Cassandra Marcussen
Learning and Testing Convex Functions
Nov 14, 2025Abstract:We consider the problems of \emph{learning} and \emph{testing} real-valued convex functions over Gaussian space. Despite the extensive study of function convexity across mathematics, statistics, and computer science, its learnability and testability have largely been examined only in discrete or restricted settings -- typically with respect to the Hamming distance, which is ill-suited for real-valued functions. In contrast, we study these problems in high dimensions under the standard Gaussian measure, assuming sample access to the function and a mild smoothness condition, namely Lipschitzness. A smoothness assumption is natural and, in fact, necessary even in one dimension: without it, convexity cannot be inferred from finitely many samples. As our main results, we give: - Learning Convex Functions: An agnostic proper learning algorithm for Lipschitz convex functions that achieves error $\varepsilon$ using $n^{O(1/\varepsilon^2)}$ samples, together with a complementary lower bound of $n^{\mathrm{poly}(1/\varepsilon)}$ samples in the \emph{correlational statistical query (CSQ)} model. - Testing Convex Functions: A tolerant (two-sided) tester for convexity of Lipschitz functions with the same sample complexity (as a corollary of our learning result), and a one-sided tester (which never rejects convex functions) using $O(\sqrt{n}/\varepsilon)^n$ samples.
Combinative Cumulative Knowledge Processes
Sep 11, 2023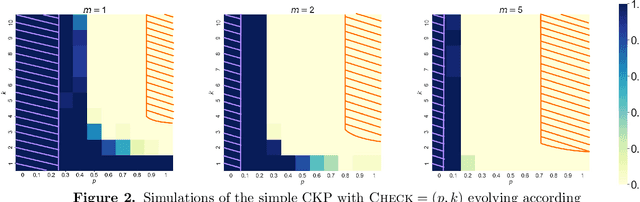
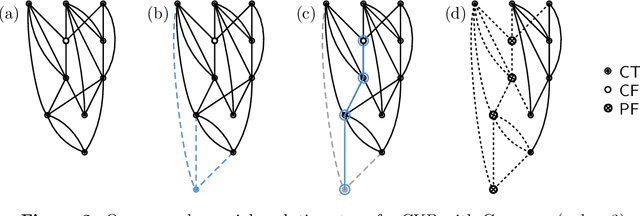
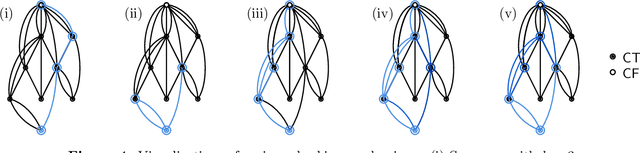
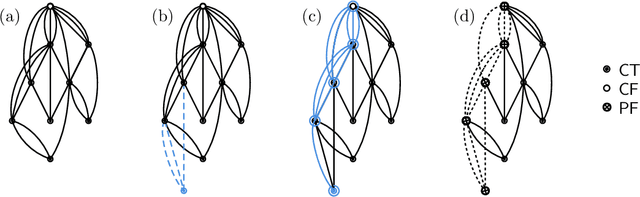
Abstract:We analyze Cumulative Knowledge Processes, introduced by Ben-Eliezer, Mikulincer, Mossel, and Sudan (ITCS 2023), in the setting of "directed acyclic graphs", i.e., when new units of knowledge may be derived by combining multiple previous units of knowledge. The main considerations in this model are the role of errors (when new units may be erroneous) and local checking (where a few antecedent units of knowledge are checked when a new unit of knowledge is discovered). The aforementioned work defined this model but only analyzed an idealized and simplified "tree-like" setting, i.e., a setting where new units of knowledge only depended directly on one previously generated unit of knowledge. The main goal of our work is to understand when the general process is safe, i.e., when the effect of errors remains under control. We provide some necessary and some sufficient conditions for safety. As in the earlier work, we demonstrate that the frequency of checking as well as the depth of the checks play a crucial role in determining safety. A key new parameter in the current work is the $\textit{combination factor}$ which is the distribution of the number of units $M$ of old knowledge that a new unit of knowledge depends on. Our results indicate that a large combination factor can compensate for a small depth of checking. The dependency of the safety on the combination factor is far from trivial. Indeed some of our main results are stated in terms of $\mathbb{E}\{1/M\}$ while others depend on $\mathbb{E}\{M\}$.
Uniformity Testing over Hypergrids with Subcube Conditioning
Feb 17, 2023Abstract:We give an algorithm for testing uniformity of distributions supported on hypergrids $[m]^n$, which makes $\tilde{O}(\text{poly}(m)\sqrt{n}/\epsilon^2)$ queries to a subcube conditional sampling oracle. When the side length $m$ of the hypergrid is a constant, our algorithm is nearly optimal and strengthens the algorithm of [CCK+21] which has the same query complexity but works for hypercubes $\{\pm 1\}^n$ only. A key technical contribution behind the analysis of our algorithm is a proof of a robust version of Pisier's inequality for functions over $\mathbb{Z}_m^n$ using Fourier analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge