Leaf Stripping on Uniform Attachment Trees

In this note we analyze the performance of a simple root-finding algorithm in uniform attachment trees. The leaf-stripping algorithm recursively removes all leaves of the tree for a carefully chosen number of rounds. We show that, with probability $1 - \epsilon$, the set of remaining vertices contains the root and has a size only depending on $\epsilon$ but not on the size of the tree.

Progress Towards Decoding Visual Imagery via fNIRS

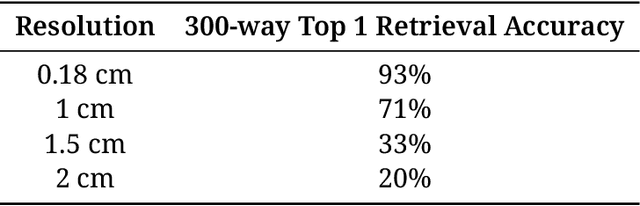
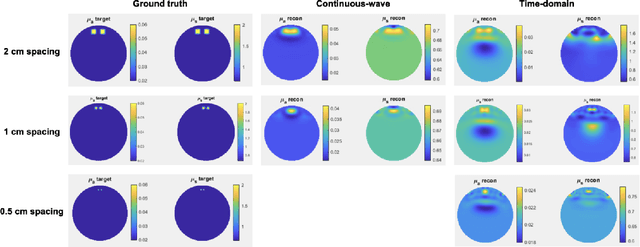
We demonstrate the possibility of reconstructing images from fNIRS brain activity and start building a prototype to match the required specs. By training an image reconstruction model on downsampled fMRI data, we discovered that cm-scale spatial resolution is sufficient for image generation. We obtained 71% retrieval accuracy with 1-cm resolution, compared to 93% on the full-resolution fMRI, and 20% with 2-cm resolution. With simulations and high-density tomography, we found that time-domain fNIRS can achieve 1-cm resolution, compared to 2-cm resolution for continuous-wave fNIRS. Lastly, we share designs for a prototype time-domain fNIRS device, consisting of a laser driver, a single photon detector, and a time-to-digital converter system.

Combinative Cumulative Knowledge Processes

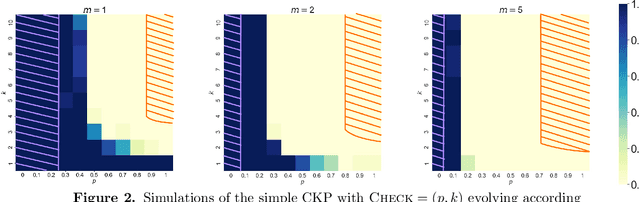
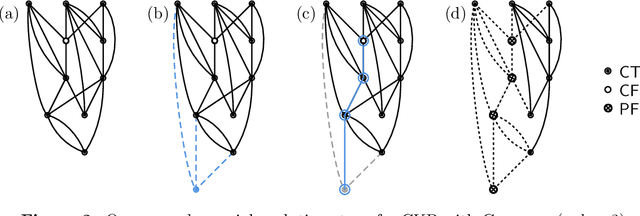
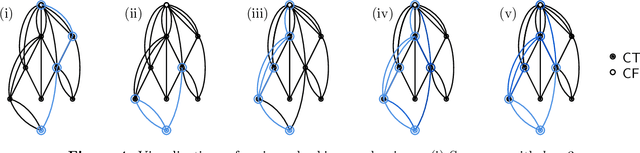
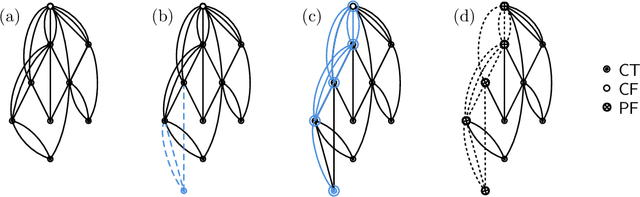
We analyze Cumulative Knowledge Processes, introduced by Ben-Eliezer, Mikulincer, Mossel, and Sudan (ITCS 2023), in the setting of "directed acyclic graphs", i.e., when new units of knowledge may be derived by combining multiple previous units of knowledge. The main considerations in this model are the role of errors (when new units may be erroneous) and local checking (where a few antecedent units of knowledge are checked when a new unit of knowledge is discovered). The aforementioned work defined this model but only analyzed an idealized and simplified "tree-like" setting, i.e., a setting where new units of knowledge only depended directly on one previously generated unit of knowledge. The main goal of our work is to understand when the general process is safe, i.e., when the effect of errors remains under control. We provide some necessary and some sufficient conditions for safety. As in the earlier work, we demonstrate that the frequency of checking as well as the depth of the checks play a crucial role in determining safety. A key new parameter in the current work is the $\textit{combination factor}$ which is the distribution of the number of units $M$ of old knowledge that a new unit of knowledge depends on. Our results indicate that a large combination factor can compensate for a small depth of checking. The dependency of the safety on the combination factor is far from trivial. Indeed some of our main results are stated in terms of $\mathbb{E}\{1/M\}$ while others depend on $\mathbb{E}\{M\}$.

A Study of Policy Gradient on a Class of Exactly Solvable Models

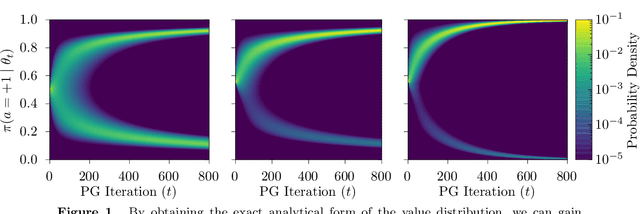
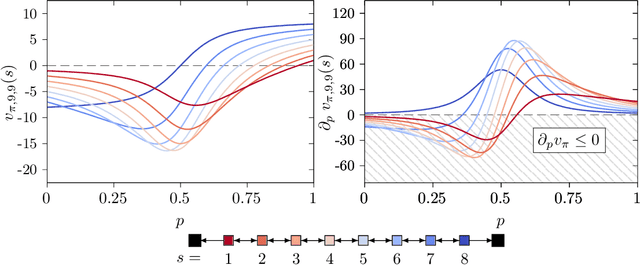
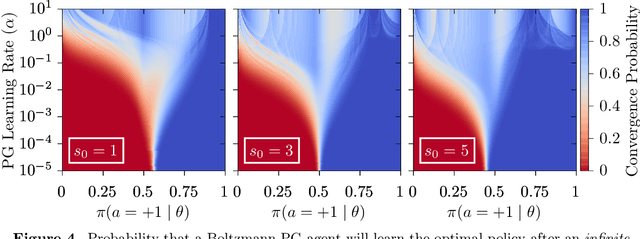
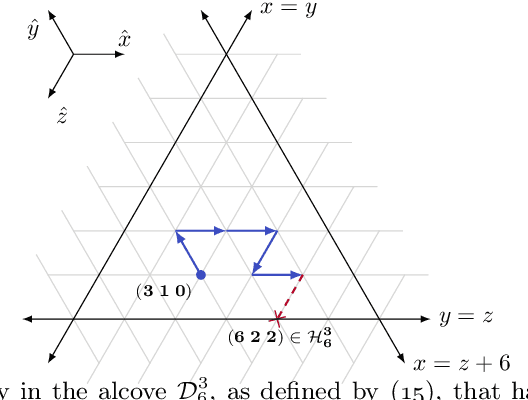
Policy gradient methods are extensively used in reinforcement learning as a way to optimize expected return. In this paper, we explore the evolution of the policy parameters, for a special class of exactly solvable POMDPs, as a continuous-state Markov chain, whose transition probabilities are determined by the gradient of the distribution of the policy's value. Our approach relies heavily on random walk theory, specifically on affine Weyl groups. We construct a class of novel partially observable environments with controllable exploration difficulty, in which the value distribution, and hence the policy parameter evolution, can be derived analytically. Using these environments, we analyze the probabilistic convergence of policy gradient to different local maxima of the value function. To our knowledge, this is the first approach developed to analytically compute the landscape of policy gradient in POMDPs for a class of such environments, leading to interesting insights into the difficulty of this problem.