Leaf Stripping on Uniform Attachment Trees

In this note we analyze the performance of a simple root-finding algorithm in uniform attachment trees. The leaf-stripping algorithm recursively removes all leaves of the tree for a carefully chosen number of rounds. We show that, with probability $1 - \epsilon$, the set of remaining vertices contains the root and has a size only depending on $\epsilon$ but not on the size of the tree.

Batched Bandits with Crowd Externalities

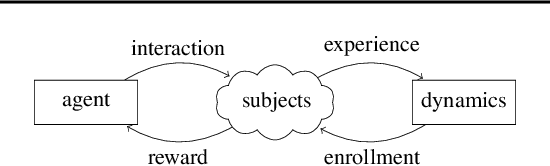
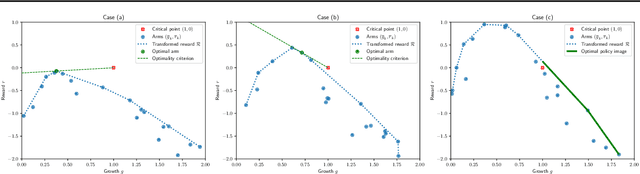
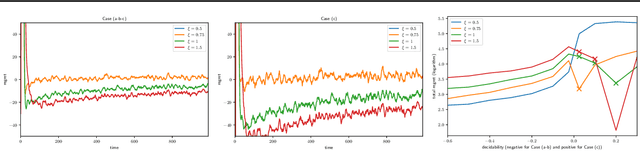
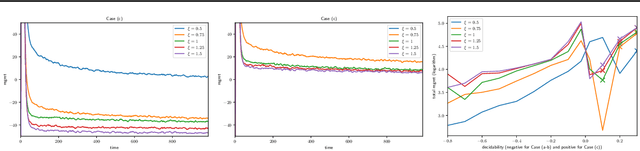
In Batched Multi-Armed Bandits (BMAB), the policy is not allowed to be updated at each time step. Usually, the setting asserts a maximum number of allowed policy updates and the algorithm schedules them so that to minimize the expected regret. In this paper, we describe a novel setting for BMAB, with the following twist: the timing of the policy update is not controlled by the BMAB algorithm, but instead the amount of data received during each batch, called \textit{crowd}, is influenced by the past selection of arms. We first design a near-optimal policy with approximate knowledge of the parameters that we prove to have a regret in $\mathcal{O}(\sqrt{\frac{\ln x}{x}}+\epsilon)$ where $x$ is the size of the crowd and $\epsilon$ is the parameter error. Next, we implement a UCB-inspired algorithm that guarantees an additional regret in $\mathcal{O}\left(\max(K\ln T,\sqrt{T\ln T})\right)$, where $K$ is the number of arms and $T$ is the horizon.