Combinative Cumulative Knowledge Processes

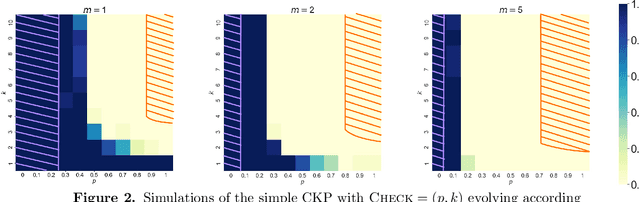
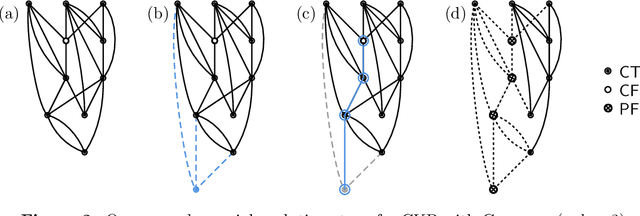
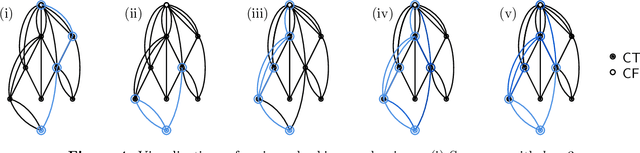
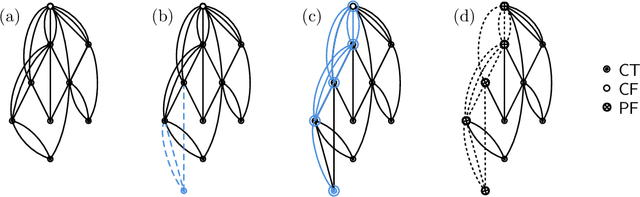
We analyze Cumulative Knowledge Processes, introduced by Ben-Eliezer, Mikulincer, Mossel, and Sudan (ITCS 2023), in the setting of "directed acyclic graphs", i.e., when new units of knowledge may be derived by combining multiple previous units of knowledge. The main considerations in this model are the role of errors (when new units may be erroneous) and local checking (where a few antecedent units of knowledge are checked when a new unit of knowledge is discovered). The aforementioned work defined this model but only analyzed an idealized and simplified "tree-like" setting, i.e., a setting where new units of knowledge only depended directly on one previously generated unit of knowledge. The main goal of our work is to understand when the general process is safe, i.e., when the effect of errors remains under control. We provide some necessary and some sufficient conditions for safety. As in the earlier work, we demonstrate that the frequency of checking as well as the depth of the checks play a crucial role in determining safety. A key new parameter in the current work is the $\textit{combination factor}$ which is the distribution of the number of units $M$ of old knowledge that a new unit of knowledge depends on. Our results indicate that a large combination factor can compensate for a small depth of checking. The dependency of the safety on the combination factor is far from trivial. Indeed some of our main results are stated in terms of $\mathbb{E}\{1/M\}$ while others depend on $\mathbb{E}\{M\}$.

Performance of the Survey Propagation-guided decimation algorithm for the random NAE-K-SAT problem

We show that the Survey Propagation-guided decimation algorithm fails to find satisfying assignments on random instances of the "Not-All-Equal-$K$-SAT" problem if the number of message passing iterations is bounded by a constant independent of the size of the instance and the clause-to-variable ratio is above $(1+o_K(1)){2^{K-1}\over K}\log^2 K$ for sufficiently large $K$. Our analysis in fact applies to a broad class of algorithms described as "sequential local algorithms". Such algorithms iteratively set variables based on some local information and then recurse on the reduced instance. Survey Propagation-guided as well as Belief Propagation-guided decimation algorithms - two widely studied message passing based algorithms, fall under this category of algorithms provided the number of message passing iterations is bounded by a constant. Another well-known algorithm falling into this category is the Unit Clause algorithm. Our work constitutes the first rigorous analysis of the performance of the SP-guided decimation algorithm. The approach underlying our paper is based on an intricate geometry of the solution space of random NAE-$K$-SAT problem. We show that above the $(1+o_K(1)){2^{K-1}\over K}\log^2 K$ threshold, the overlap structure of $m$-tuples of satisfying assignments exhibit a certain clustering behavior expressed in the form of constraints on distances between the $m$ assignments, for appropriately chosen $m$. We further show that if a sequential local algorithm succeeds in finding a satisfying assignment with probability bounded away from zero, then one can construct an $m$-tuple of solutions violating these constraints, thus leading to a contradiction. Along with (citation), this result is the first work which directly links the clustering property of random constraint satisfaction problems to the computational hardness of finding satisfying assignments.