Size and depth of monotone neural networks: interpolation and approximation

Monotone functions and data sets arise in a variety of applications. We study the interpolation problem for monotone data sets: The input is a monotone data set with $n$ points, and the goal is to find a size and depth efficient monotone neural network, with non negative parameters and threshold units, that interpolates the data set. We show that there are monotone data sets that cannot be interpolated by a monotone network of depth $2$. On the other hand, we prove that for every monotone data set with $n$ points in $\mathbb{R}^d$, there exists an interpolating monotone network of depth $4$ and size $O(nd)$. Our interpolation result implies that every monotone function over $[0,1]^d$ can be approximated arbitrarily well by a depth-4 monotone network, improving the previous best-known construction of depth $d+1$. Finally, building on results from Boolean circuit complexity, we show that the inductive bias of having positive parameters can lead to a super-polynomial blow-up in the number of neurons when approximating monotone functions.

Non-asymptotic approximations of neural networks by Gaussian processes

We study the extent to which wide neural networks may be approximated by Gaussian processes when initialized with random weights. It is a well-established fact that as the width of a network goes to infinity, its law converges to that of a Gaussian process. We make this quantitative by establishing explicit convergence rates for the central limit theorem in an infinite-dimensional functional space, metrized with a natural transportation distance. We identify two regimes of interest; when the activation function is polynomial, its degree determines the rate of convergence, while for non-polynomial activations, the rate is governed by the smoothness of the function.

Community detection and percolation of information in a geometric setting

We make the first steps towards generalizing the theory of stochastic block models, in the sparse regime, towards a model where the discrete community structure is replaced by an underlying geometry. We consider a geometric random graph over a homogeneous metric space where the probability of two vertices to be connected is an arbitrary function of the distance. We give sufficient conditions under which the locations can be recovered (up to an isomorphism of the space) in the sparse regime. Moreover, we define a geometric counterpart of the model of flow of information on trees, due to Mossel and Peres, in which one considers a branching random walk on a sphere and the goal is to recover the location of the root based on the locations of leaves. We give some sufficient conditions for percolation and for non-percolation of information in this model.

Network size and weights size for memorization with two-layers neural networks

In 1988, Eric B. Baum showed that two-layers neural networks with threshold activation function can perfectly memorize the binary labels of $n$ points in general position in $\mathbb{R}^d$ using only $\ulcorner n/d \urcorner$ neurons. We observe that with ReLU networks, using four times as many neurons one can fit arbitrary real labels. Moreover, for approximate memorization up to error $\epsilon$, the neural tangent kernel can also memorize with only $O\left(\frac{n}{d} \cdot \log(1/\epsilon) \right)$ neurons (assuming that the data is well dispersed too). We show however that these constructions give rise to networks where the magnitude of the neurons' weights are far from optimal. In contrast we propose a new training procedure for ReLU networks, based on complex (as opposed to real) recombination of the neurons, for which we show approximate memorization with both $O\left(\frac{n}{d} \cdot \frac{\log(1/\epsilon)}{\epsilon}\right)$ neurons, as well as nearly-optimal size of the weights.

How to trap a gradient flow

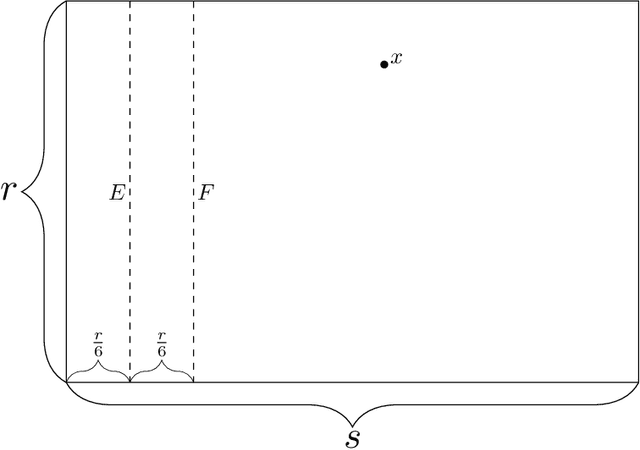
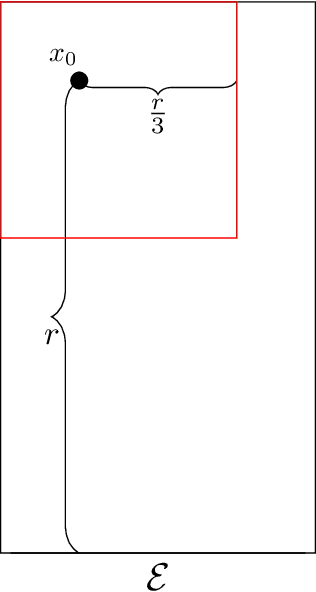
We consider the problem of finding an $\varepsilon$-approximate stationary point of a smooth function on a compact domain of $\mathbb{R}^d$. In contrast with dimension-free approaches such as gradient descent, we focus here on the case where $d$ is finite, and potentially small. This viewpoint was explored in 1993 by Vavasis, who proposed an algorithm which, for any fixed finite dimension $d$, improves upon the $O(1/\varepsilon^2)$ oracle complexity of gradient descent. For example for $d=2$, Vavasis' approach obtains the complexity $O(1/\varepsilon)$. Moreover for $d=2$ he also proved a lower bound of $\Omega(1/\sqrt{\varepsilon})$ for deterministic algorithms (we extend this result to randomized algorithms). Our main contribution is an algorithm, which we call gradient flow trapping (GFT), and the analysis of its oracle complexity. In dimension $d=2$, GFT closes the gap with Vavasis' lower bound (up to a logarithmic factor), as we show that it has complexity $O\left(\sqrt{\frac{\log(1/\varepsilon)}{\varepsilon}}\right)$. In dimension $d=3$, we show a complexity of $O\left(\frac{\log(1/\varepsilon)}{\varepsilon}\right)$, improving upon Vavasis' $O\left(1 / \varepsilon^{1.2} \right)$. In higher dimensions, GFT has the remarkable property of being a logarithmic parallel depth strategy, in stark contrast with the polynomial depth of gradient descent or Vavasis' algorithm. In this higher dimensional regime, the total work of GFT improves quadratically upon the only other known polylogarithmic depth strategy for this problem, namely naive grid search.