Efficient Reconstruction of Stochastic Pedigrees: Some Steps From Theory to Practice
Paper and Code
Apr 10, 2022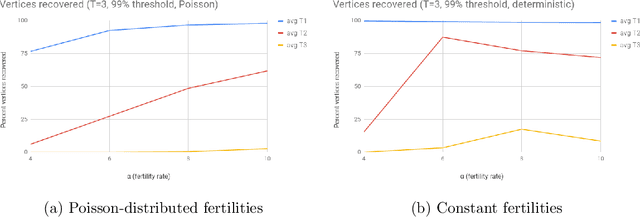
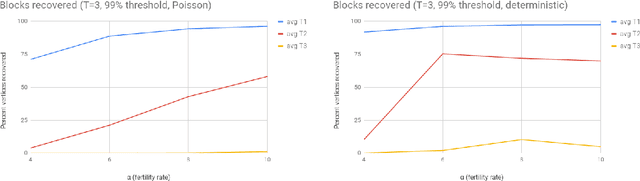
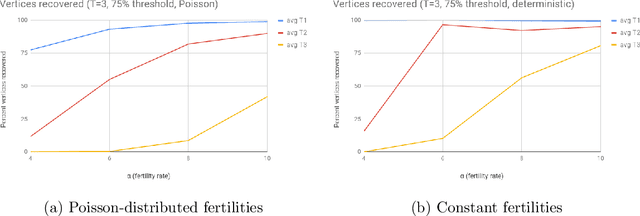
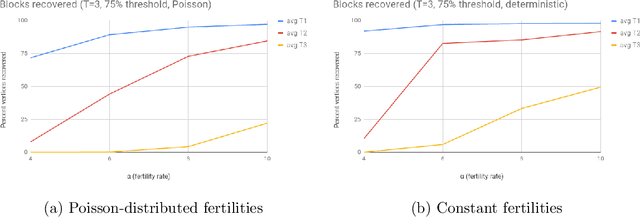
In an extant population, how much information do extant individuals provide on the pedigree of their ancestors? Recent work by Kim, Mossel, Ramnarayan and Turner (2020) studied this question under a number of simplifying assumptions, including random mating, fixed length inheritance blocks and sufficiently large founding population. They showed that under these conditions if the average number of offspring is a sufficiently large constant, then it is possible to recover a large fraction of the pedigree structure and genetic content by an algorithm they named REC-GEN. We are interested in studying the performance of REC-GEN on simulated data generated according to the model. As a first step, we improve the running time of the algorithm. However, we observe that even the faster version of the algorithm does not do well in any simulations in recovering the pedigree beyond 2 generations. We claim that this is due to the inbreeding present in any setting where the algorithm can be run, even on simulated data. To support the claim we show that a main step of the algorithm, called ancestral reconstruction, performs accurately in a idealized setting with no inbreeding but performs poorly in random mating populations. To overcome the poor behavior of REC-GEN we introduce a Belief-Propagation based heuristic that accounts for the inbreeding and performs much better in our simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge