Stochastic Gradient Flow Dynamics of Test Risk and its Exact Solution for Weak Features

We investigate the test risk of continuous-time stochastic gradient flow dynamics in learning theory. Using a path integral formulation we provide, in the regime of a small learning rate, a general formula for computing the difference between test risk curves of pure gradient and stochastic gradient flows. We apply the general theory to a simple model of weak features, which displays the double descent phenomenon, and explicitly compute the corrections brought about by the added stochastic term in the dynamics, as a function of time and model parameters. The analytical results are compared to simulations of discrete-time stochastic gradient descent and show good agreement.

Learning curves for the multi-class teacher-student perceptron

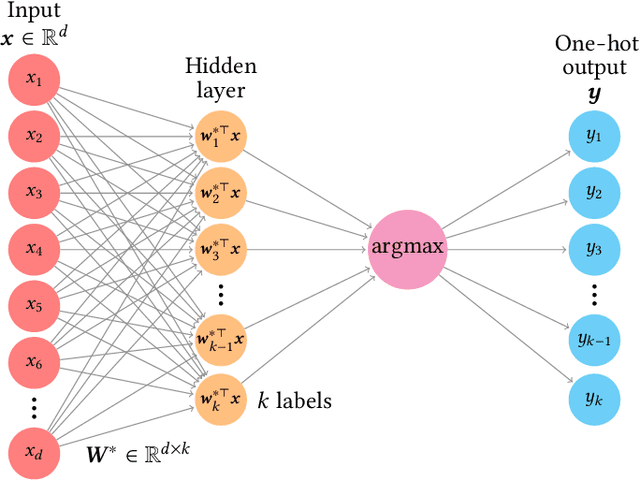
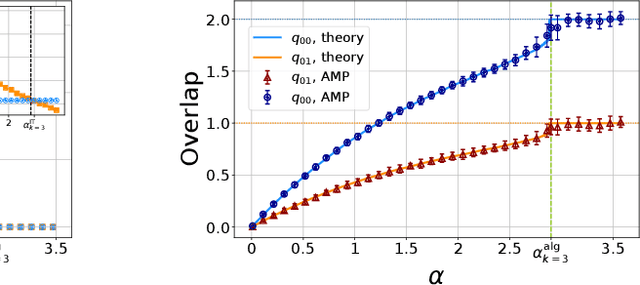
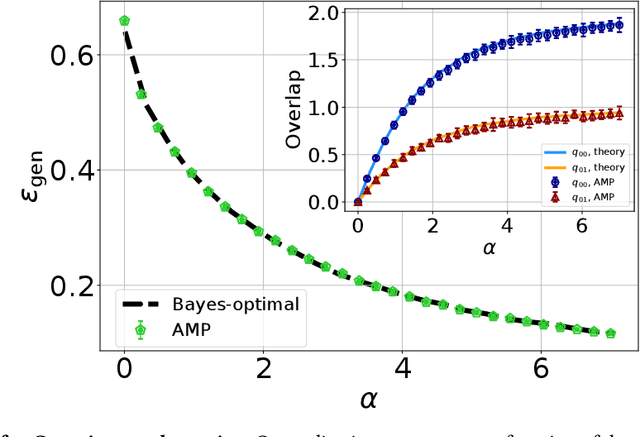
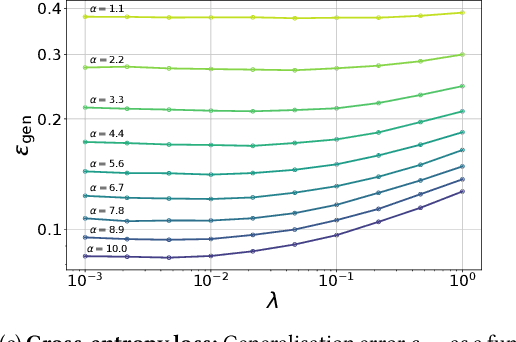
One of the most classical results in high-dimensional learning theory provides a closed-form expression for the generalisation error of binary classification with the single-layer teacher-student perceptron on i.i.d. Gaussian inputs. Both Bayes-optimal estimation and empirical risk minimisation (ERM) were extensively analysed for this setting. At the same time, a considerable part of modern machine learning practice concerns multi-class classification. Yet, an analogous analysis for the corresponding multi-class teacher-student perceptron was missing. In this manuscript we fill this gap by deriving and evaluating asymptotic expressions for both the Bayes-optimal and ERM generalisation errors in the high-dimensional regime. For Gaussian teacher weights, we investigate the performance of ERM with both cross-entropy and square losses, and explore the role of ridge regularisation in approaching Bayes-optimality. In particular, we observe that regularised cross-entropy minimisation yields close-to-optimal accuracy. Instead, for a binary teacher we show that a first-order phase transition arises in the Bayes-optimal performance.

Phase diagram of Stochastic Gradient Descent in high-dimensional two-layer neural networks

Despite the non-convex optimization landscape, over-parametrized shallow networks are able to achieve global convergence under gradient descent. The picture can be radically different for narrow networks, which tend to get stuck in badly-generalizing local minima. Here we investigate the cross-over between these two regimes in the high-dimensional setting, and in particular investigate the connection between the so-called mean-field/hydrodynamic regime and the seminal approach of Saad & Solla. Focusing on the case of Gaussian data, we study the interplay between the learning rate, the time scale, and the number of hidden units in the high-dimensional dynamics of stochastic gradient descent (SGD). Our work builds on a deterministic description of SGD in high-dimensions from statistical physics, which we extend and for which we provide rigorous convergence rates.

Restricted Boltzmann Machine Flows and The Critical Temperature of Ising models

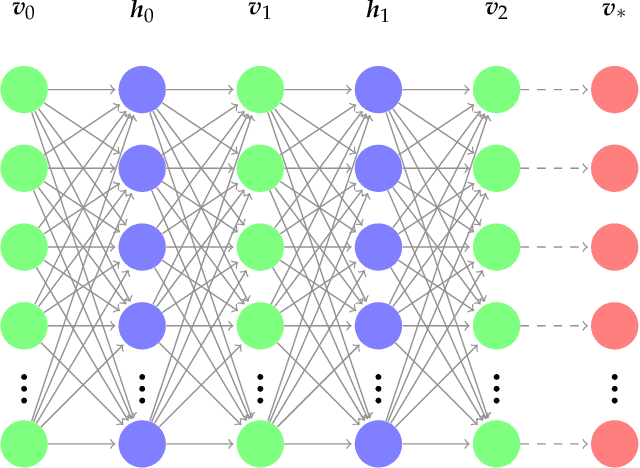
We explore alternative experimental setups for the iterative sampling (flow) from Restricted Boltzmann Machines (RBM) mapped on the temperature space of square lattice Ising models by a neural network thermometer. This framework has been introduced to explore connections between RBM-based deep neural networks and the Renormalization Group (RG). It has been found that, under certain conditions, the flow of an RBM trained with Ising spin configurations approaches in the temperature space a value around the critical one: $ k_B T_c / J \approx 2.269$. In this paper we consider datasets with no information about model topology to argue that a neural network thermometer is not an accurate way to detect whether the RBM has learned scale invariance or not.