Pierfrancesco Urbani
Dynamical Decoupling of Generalization and Overfitting in Large Two-Layer Networks
Feb 28, 2025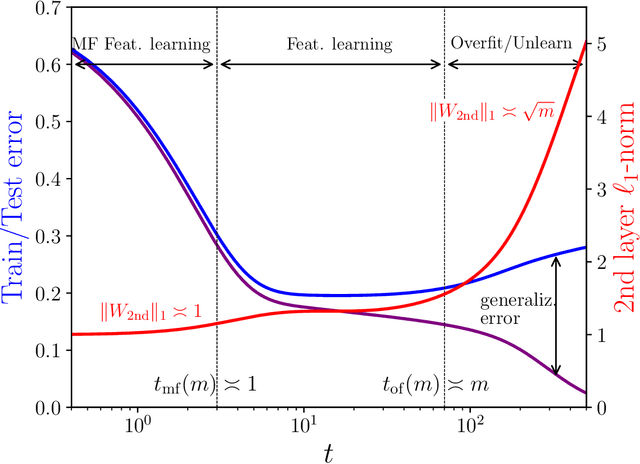
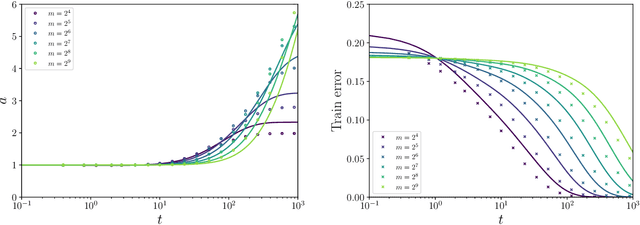
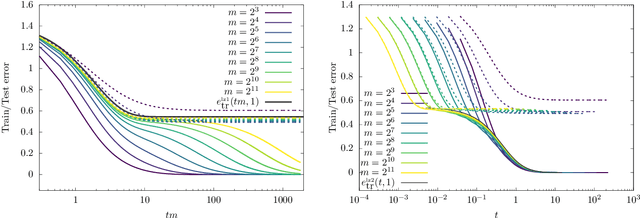
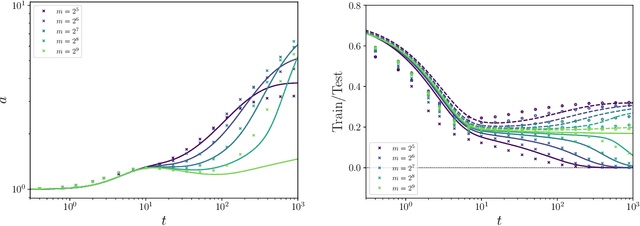
Abstract:The inductive bias and generalization properties of large machine learning models are -- to a substantial extent -- a byproduct of the optimization algorithm used for training. Among others, the scale of the random initialization, the learning rate, and early stopping all have crucial impact on the quality of the model learnt by stochastic gradient descent or related algorithms. In order to understand these phenomena, we study the training dynamics of large two-layer neural networks. We use a well-established technique from non-equilibrium statistical physics (dynamical mean field theory) to obtain an asymptotic high-dimensional characterization of this dynamics. This characterization applies to a Gaussian approximation of the hidden neurons non-linearity, and empirically captures well the behavior of actual neural network models. Our analysis uncovers several interesting new phenomena in the training dynamics: $(i)$ The emergence of a slow time scale associated with the growth in Gaussian/Rademacher complexity; $(ii)$ As a consequence, algorithmic inductive bias towards small complexity, but only if the initialization has small enough complexity; $(iii)$ A separation of time scales between feature learning and overfitting; $(iv)$ A non-monotone behavior of the test error and, correspondingly, a `feature unlearning' phase at large times.
Generative modeling through internal high-dimensional chaotic activity
May 17, 2024



Abstract:Generative modeling aims at producing new datapoints whose statistical properties resemble the ones in a training dataset. In recent years, there has been a burst of machine learning techniques and settings that can achieve this goal with remarkable performances. In most of these settings, one uses the training dataset in conjunction with noise, which is added as a source of statistical variability and is essential for the generative task. Here, we explore the idea of using internal chaotic dynamics in high-dimensional chaotic systems as a way to generate new datapoints from a training dataset. We show that simple learning rules can achieve this goal within a set of vanilla architectures and characterize the quality of the generated datapoints through standard accuracy measures.
Stochastic Gradient Descent outperforms Gradient Descent in recovering a high-dimensional signal in a glassy energy landscape
Sep 09, 2023


Abstract:Stochastic Gradient Descent (SGD) is an out-of-equilibrium algorithm used extensively to train artificial neural networks. However very little is known on to what extent SGD is crucial for to the success of this technology and, in particular, how much it is effective in optimizing high-dimensional non-convex cost functions as compared to other optimization algorithms such as Gradient Descent (GD). In this work we leverage dynamical mean field theory to analyze exactly its performances in the high-dimensional limit. We consider the problem of recovering a hidden high-dimensional non-linearly encrypted signal, a prototype high-dimensional non-convex hard optimization problem. We compare the performances of SGD to GD and we show that SGD largely outperforms GD. In particular, a power law fit of the relaxation time of these algorithms shows that the recovery threshold for SGD with small batch size is smaller than the corresponding one of GD.
The effective noise of Stochastic Gradient Descent
Dec 20, 2021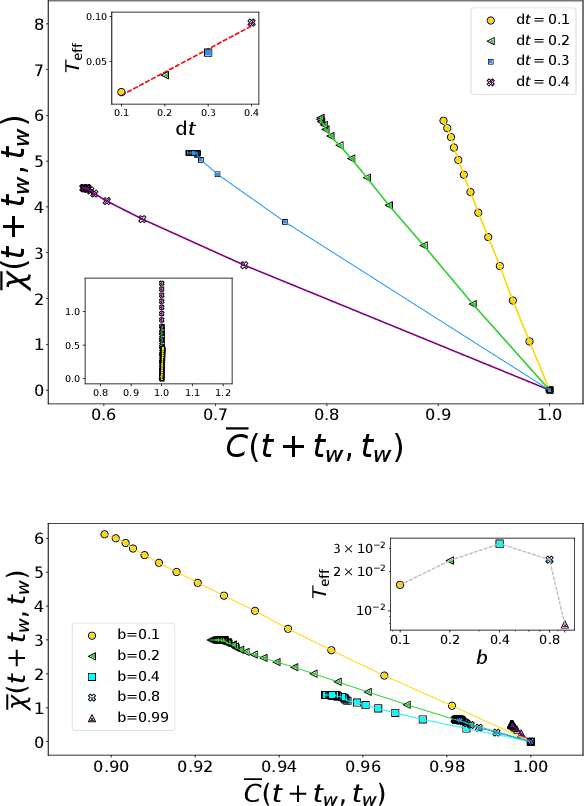

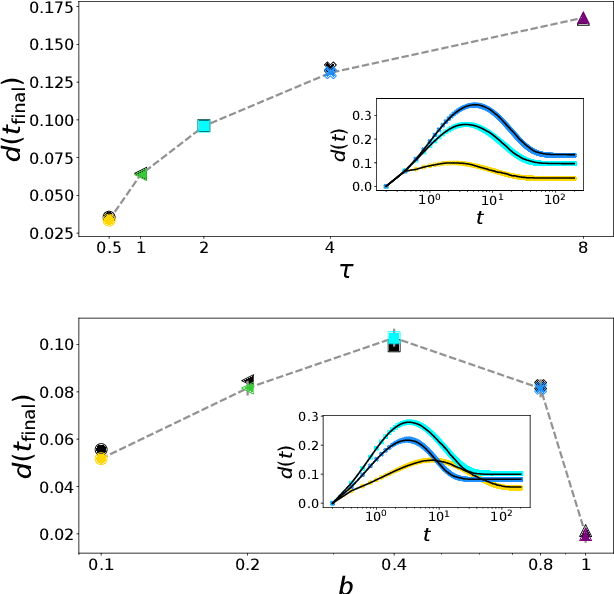
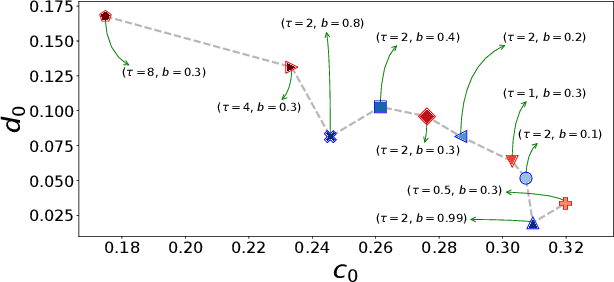
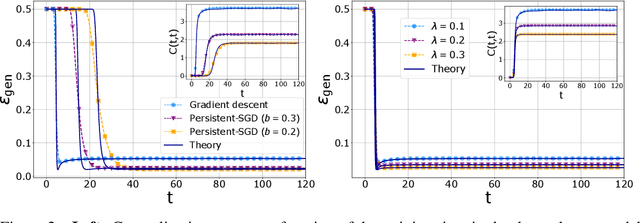
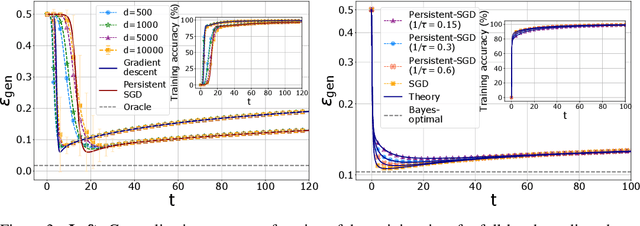
Abstract:Stochastic Gradient Descent (SGD) is the workhorse algorithm of deep learning technology. At each step of the training phase, a mini batch of samples is drawn from the training dataset and the weights of the neural network are adjusted according to the performance on this specific subset of examples. The mini-batch sampling procedure introduces a stochastic dynamics to the gradient descent, with a non-trivial state-dependent noise. We characterize the stochasticity of SGD and a recently-introduced variant, persistent SGD, in a prototypical neural network model. In the under-parametrized regime, where the final training error is positive, the SGD dynamics reaches a stationary state and we define an effective temperature from the fluctuation-dissipation theorem, computed from dynamical mean-field theory. We use the effective temperature to quantify the magnitude of the SGD noise as a function of the problem parameters. In the over-parametrized regime, where the training error vanishes, we measure the noise magnitude of SGD by computing the average distance between two replicas of the system with the same initialization and two different realizations of SGD noise. We find that the two noise measures behave similarly as a function of the problem parameters. Moreover, we observe that noisier algorithms lead to wider decision boundaries of the corresponding constraint satisfaction problem.
Just a Momentum: Analytical Study of Momentum-Based Acceleration Methods in Paradigmatic High-Dimensional Non-Convex Problems
Mar 11, 2021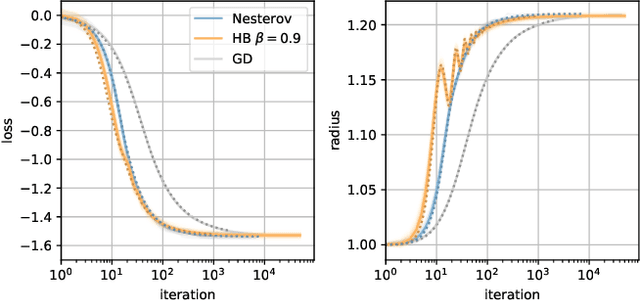
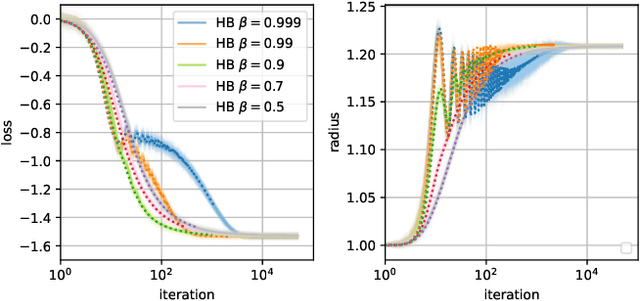
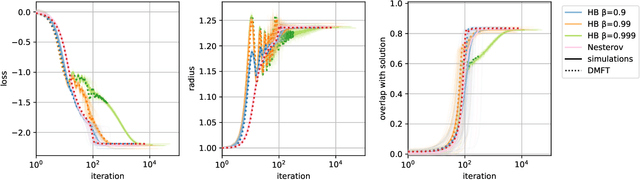
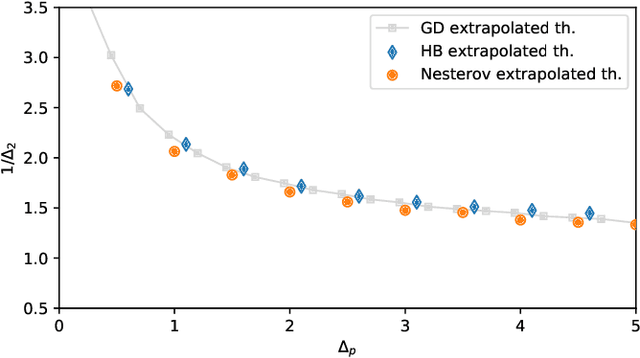
Abstract:When optimizing over loss functions it is common practice to use momentum-based accelerated methods rather than vanilla gradient-based method. Despite widely applied to arbitrary loss function, their behaviour in generically non-convex, high dimensional landscapes is poorly understood. In this work we used dynamical mean field theory techniques to describe analytically the average behaviour of these methods in a prototypical non-convex model: the (spiked) matrix-tensor model. We derive a closed set of equations that describe the behaviours of several algorithms including heavy-ball momentum and Nesterov acceleration. Additionally we characterize the evolution of a mathematically equivalent physical system of massive particles relaxing toward the bottom of an energetic landscape. Under the correct mapping the two dynamics are equivalent and it can be noticed that having a large mass increases the effective time step of the heavy ball dynamics leading to a speed up.
Stochasticity helps to navigate rough landscapes: comparing gradient-descent-based algorithms in the phase retrieval problem
Mar 08, 2021
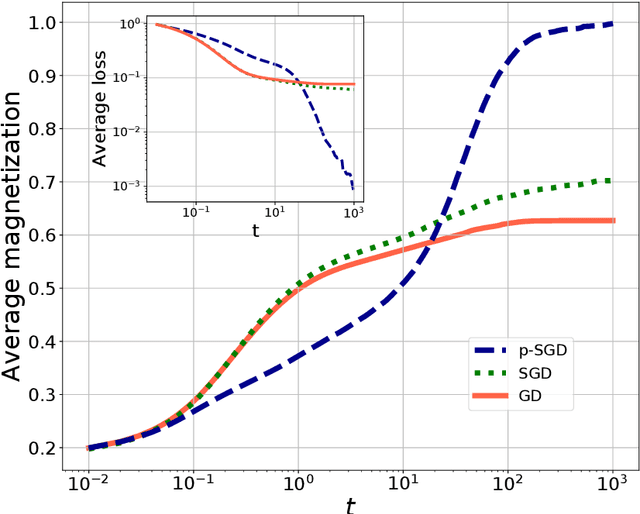
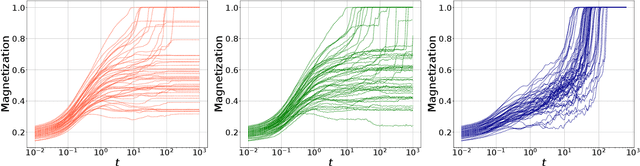
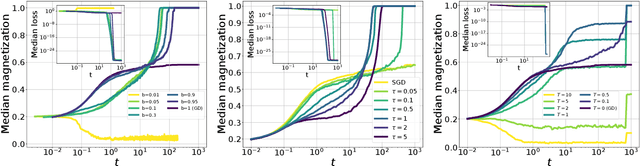
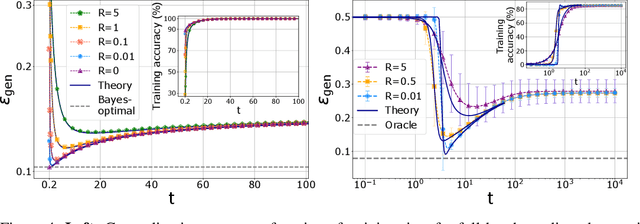
Abstract:In this paper we investigate how gradient-based algorithms such as gradient descent, (multi-pass) stochastic gradient descent, its persistent variant, and the Langevin algorithm navigate non-convex losslandscapes and which of them is able to reach the best generalization error at limited sample complexity. We consider the loss landscape of the high-dimensional phase retrieval problem as a prototypical highly non-convex example. We observe that for phase retrieval the stochastic variants of gradient descent are able to reach perfect generalization for regions of control parameters where the gradient descent algorithm is not. We apply dynamical mean-field theory from statistical physics to characterize analytically the full trajectories of these algorithms in their continuous-time limit, with a warm start, and for large system sizes. We further unveil several intriguing properties of the landscape and the algorithms such as that the gradient descent can obtain better generalization properties from less informed initializations.
Complex Dynamics in Simple Neural Networks: Understanding Gradient Flow in Phase Retrieval
Jun 12, 2020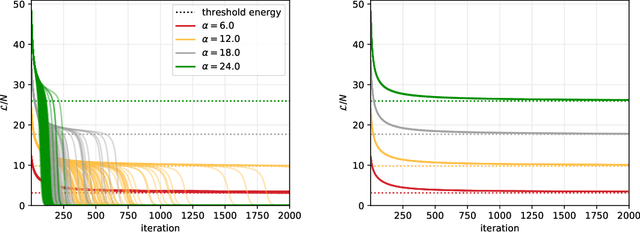
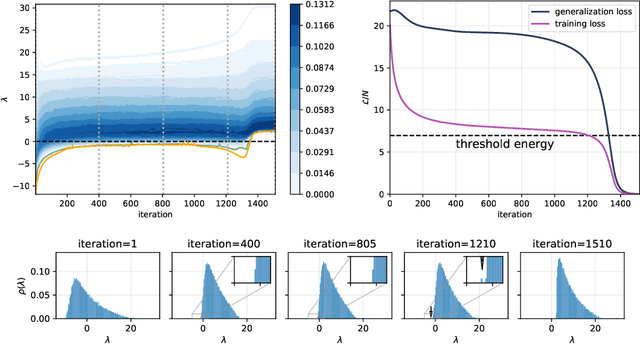
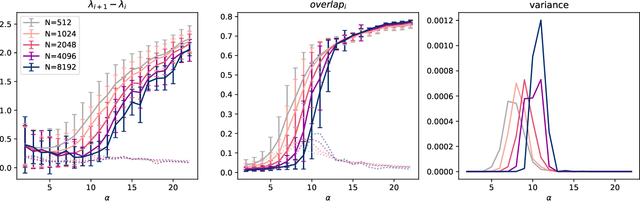
Abstract:Despite the widespread use of gradient-based algorithms for optimizing high-dimensional non-convex functions, understanding their ability of finding good minima instead of being trapped in spurious ones remains to a large extent an open problem. Here we focus on gradient flow dynamics for phase retrieval from random measurements. When the ratio of the number of measurements over the input dimension is small the dynamics remains trapped in spurious minima with large basins of attraction. We find analytically that above a critical ratio those critical points become unstable developing a negative direction toward the signal. By numerical experiments we show that in this regime the gradient flow algorithm is not trapped; it drifts away from the spurious critical points along the unstable direction and succeeds in finding the global minimum. Using tools from statistical physics we characterize this phenomenon, which is related to a BBP-type transition in the Hessian of the spurious minima.
Dynamical mean-field theory for stochastic gradient descent in Gaussian mixture classification
Jun 10, 2020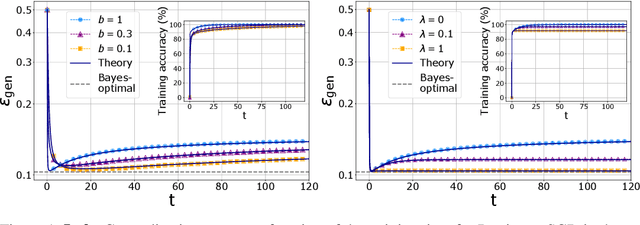
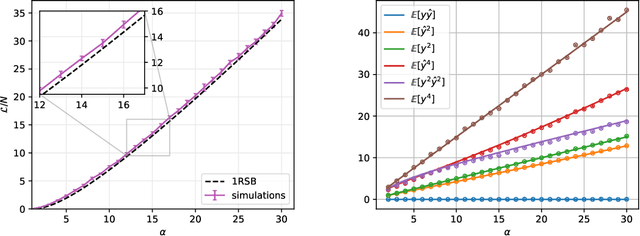
Abstract:We analyze in a closed form the learning dynamics of stochastic gradient descent (SGD) for a single layer neural network classifying a high-dimensional Gaussian mixture where each cluster is assigned one of two labels. This problem provides a prototype of a non-convex loss landscape with interpolating regimes and a large generalization gap. We define a particular stochastic process for which SGD can be extended to a continuous-time limit that we call stochastic gradient flow. In the full-batch limit we recover the standard gradient flow. We apply dynamical mean-field theory from statistical physics to track the dynamics of the algorithm in the high-dimensional limit via a self-consistent stochastic process. We explore the performance of the algorithm as a function of control parameters shedding light on how it navigates the loss landscape.
Passed & Spurious: analysing descent algorithms and local minima in spiked matrix-tensor model
Feb 01, 2019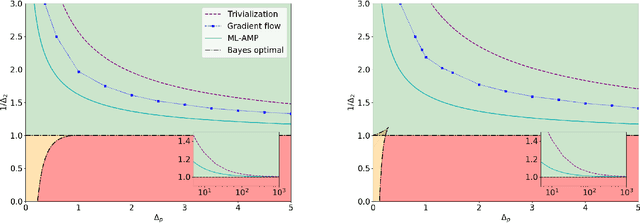
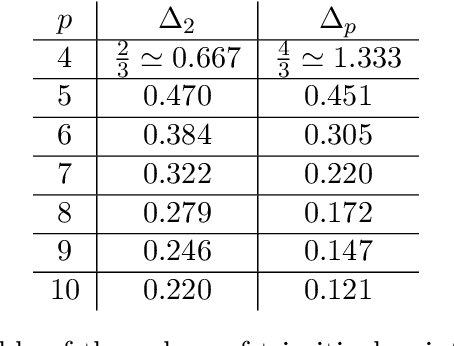
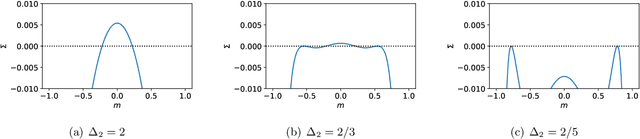
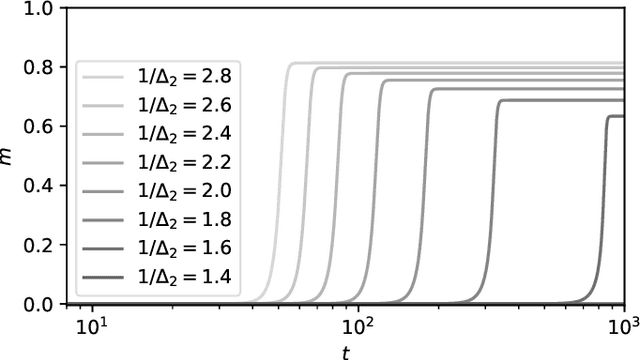
Abstract:In this work we analyse quantitatively the interplay between the loss landscape and performance of descent algorithms in a prototypical inference problem, the spiked matrix-tensor model. We study a loss function that is the negative log-likelihood of the model. We analyse the number of local minima at a fixed distance from the signal/spike with the Kac-Rice formula, and locate trivialization of the landscape at large signal-to-noise ratios. We evaluate in a closed form the performance of a gradient flow algorithm using integro-differential PDEs as developed in physics of disordered systems for the Langevin dynamics. We analyze the performance of an approximate message passing algorithm estimating the maximum likelihood configuration via its state evolution. We conclude by comparing the above results: while we observe a drastic slow down of the gradient flow dynamics even in the region where the landscape is trivial, both the analyzed algorithms are shown to perform well even in the part of the region of parameters where spurious local minima are present.
Marvels and Pitfalls of the Langevin Algorithm in Noisy High-dimensional Inference
Dec 21, 2018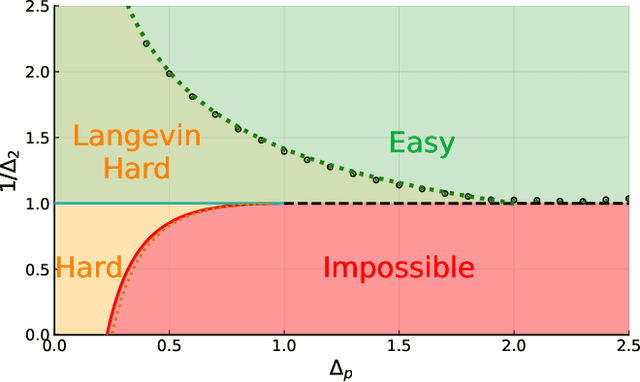
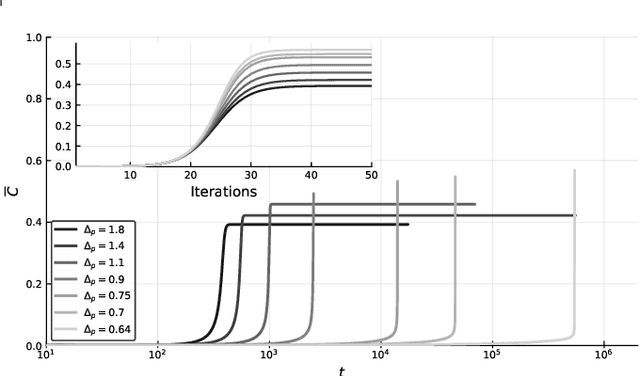
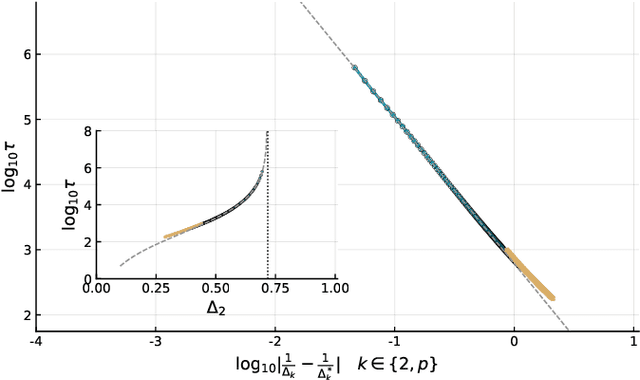
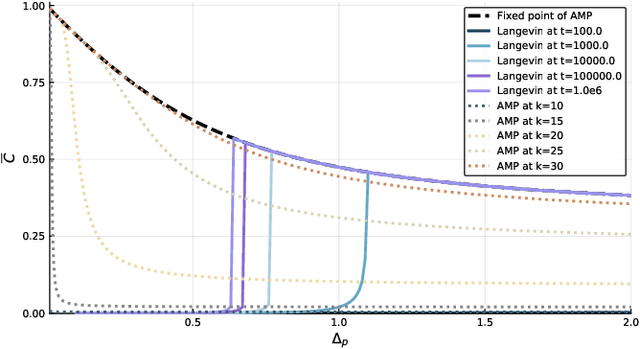
Abstract:Gradient-descent-based algorithms and their stochastic versions have widespread applications in machine learning and statistical inference. In this work we perform an analytic study of the performances of one of them, the Langevin algorithm, in the context of noisy high-dimensional inference. We employ the Langevin algorithm to sample the posterior probability measure for the spiked matrix-tensor model. The typical behaviour of this algorithm is described by a system of integro-differential equations that we call the Langevin state evolution, whose solution is compared with the one of the state evolution of approximate message passing (AMP). Our results show that, remarkably, the algorithmic threshold of the Langevin algorithm is sub-optimal with respect to the one given by AMP. We conjecture this phenomenon to be due to the residual glassiness present in that region of parameters. Finally we show how a landscape-annealing protocol, that uses the Langevin algorithm but violate the Bayes-optimality condition, can approach the performance of AMP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge