Connecting NTK and NNGP: A Unified Theoretical Framework for Neural Network Learning Dynamics in the Kernel Regime

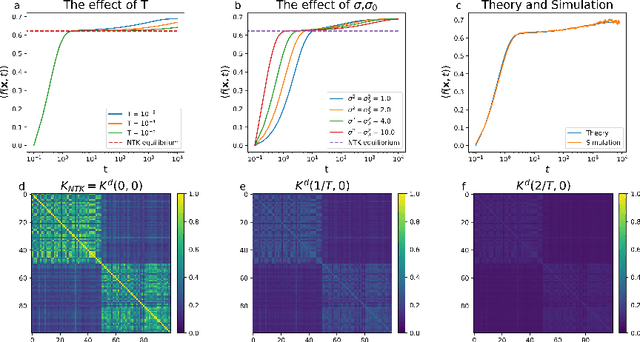
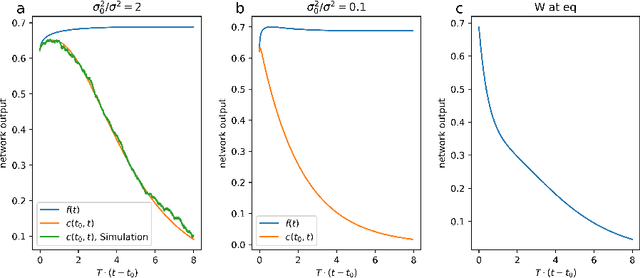
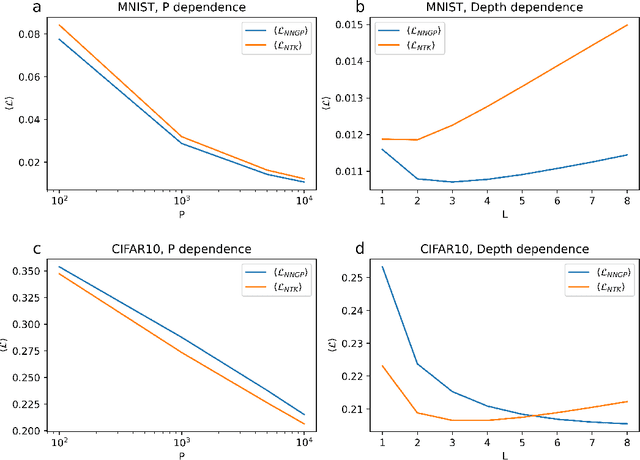
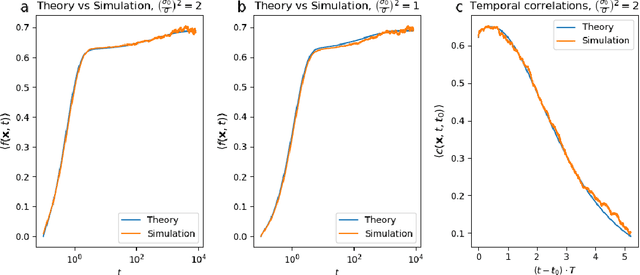
Artificial neural networks have revolutionized machine learning in recent years, but a complete theoretical framework for their learning process is still lacking. Substantial progress has been made for infinitely wide networks. In this regime, two disparate theoretical frameworks have been used, in which the network's output is described using kernels: one framework is based on the Neural Tangent Kernel (NTK) which assumes linearized gradient descent dynamics, while the Neural Network Gaussian Process (NNGP) kernel assumes a Bayesian framework. However, the relation between these two frameworks has remained elusive. This work unifies these two distinct theories using a Markov proximal learning model for learning dynamics in an ensemble of randomly initialized infinitely wide deep networks. We derive an exact analytical expression for the network input-output function during and after learning, and introduce a new time-dependent Neural Dynamical Kernel (NDK) from which both NTK and NNGP kernels can be derived. We identify two learning phases characterized by different time scales: gradient-driven and diffusive learning. In the initial gradient-driven learning phase, the dynamics is dominated by deterministic gradient descent, and is described by the NTK theory. This phase is followed by the diffusive learning stage, during which the network parameters sample the solution space, ultimately approaching the equilibrium distribution corresponding to NNGP. Combined with numerical evaluations on synthetic and benchmark datasets, we provide novel insights into the different roles of initialization, regularization, and network depth, as well as phenomena such as early stopping and representational drift. This work closes the gap between the NTK and NNGP theories, providing a comprehensive framework for understanding the learning process of deep neural networks in the infinite width limit.

Naive Artificial Intelligence

In the cognitive sciences, it is common to distinguish between crystal intelligence, the ability to utilize knowledge acquired through past learning or experience and fluid intelligence, the ability to solve novel problems without relying on prior knowledge. Using this cognitive distinction between the two types of intelligence, extensively-trained deep networks that can play chess or Go exhibit crystal but not fluid intelligence. In humans, fluid intelligence is typically studied and quantified using intelligence tests. Previous studies have shown that deep networks can solve some forms of intelligence tests, but only after extensive training. Here we present a computational model that solves intelligence tests without any prior training. This ability is based on continual inductive reasoning, and is implemented by deep unsupervised latent-prediction networks. Our work demonstrates the potential fluid intelligence of deep networks. Finally, we propose that the computational principles underlying our approach can be used to model fluid intelligence in the cognitive sciences.