Subject Matter Expertise vs Professional Management in Collective Sequential Decision Making

Your company's CEO is retiring. You search for a successor. You can promote an employee from the company familiar with the company's operations, or recruit an external professional manager. Who should you prefer? It has not been clear how to address this question, the "subject matter expertise vs. professional manager debate", quantitatively and objectively. We note that a company's success depends on long sequences of interdependent decisions, with often-opposing recommendations of diverse board members. To model this task in a controlled environment, we utilize chess - a complex, sequential game with interdependent decisions which allows for quantitative analysis of performance and expertise (since the states, actions and game outcomes are well-defined). The availability of chess engines differing in style and expertise, allows scalable experimentation. We considered a team of (computer) chess players. At each turn, team members recommend a move and a manager chooses a recommendation. We compared the performance of two manager types. For manager as "subject matter expert", we used another (computer) chess player that assesses the recommendations of the team members based on its own chess expertise. We examined the performance of such managers at different strength levels. To model a "professional manager", we used Reinforcement Learning (RL) to train a network that identifies the board positions in which different team members have relative advantage, without any pretraining in chess. We further examined this network to see if any chess knowledge is acquired implicitly. We found that subject matter expertise beyond a minimal threshold does not significantly contribute to team synergy. Moreover, performance of a RL-trained "professional" manager significantly exceeds that of even the best "expert" managers, while acquiring only limited understanding of chess.

Is there Value in Reinforcement Learning?

Action-values play a central role in popular Reinforcement Learing (RL) models of behavior. Yet, the idea that action-values are explicitly represented has been extensively debated. Critics had therefore repeatedly suggested that policy-gradient (PG) models should be favored over value-based (VB) ones, as a potential solution for this dilemma. Here we argue that this solution is unsatisfying. This is because PG methods are not, in fact, "Value-free" -- while they do not rely on an explicit representation of Value for acting (stimulus-response mapping), they do require it for learning. Hence, switching to PG models is, per se, insufficient for eliminating Value from models of behavior. More broadly, the requirement for a representation of Value stems from the underlying assumptions regarding the optimization objective posed by the standard RL framework, not from the particular algorithm chosen to solve it. Previous studies mostly took these standard RL assumptions for granted, as part of their conceptualization or problem modeling, while debating the different methods used to optimize it (i.e., PG or VB). We propose that, instead, the focus of the debate should shift to critically evaluating the underlying modeling assumptions. Such evaluation is particularly important from an experimental perspective. Indeed, the very notion of Value must be reconsidered when standard assumptions (e.g., risk neutrality, full-observability, Markovian environment, exponential discounting) are relaxed, as is likely in natural settings. Finally, we use the Value debate as a case study to argue in favor of a more nuanced, algorithmic rather than statistical, view of what constitutes "a model" in cognitive sciences. Our analysis suggests that besides "parametric" statistical complexity, additional aspects such as computational complexity must also be taken into account when evaluating model complexity.

Investigating learning-independent abstract reasoning in artificial neural networks

Humans are capable of solving complex abstract reasoning tests. Whether this ability reflects a learning-independent inference mechanism applicable to any novel unlearned problem or whether it is a manifestation of extensive training throughout life is an open question. Addressing this question in humans is challenging because it is impossible to control their prior training. However, assuming a similarity between the cognitive processing of Artificial Neural Networks (ANNs) and humans, the extent to which training is required for ANNs' abstract reasoning is informative about this question in humans. Previous studies demonstrated that ANNs can solve abstract reasoning tests. However, this success required extensive training. In this study, we examined the learning-independent abstract reasoning of ANNs. Specifically, we evaluated their performance without any pretraining, with the ANNs' weights being randomly-initialized, and only change in the process of problem solving. We found that naive ANN models can solve non-trivial visual reasoning tests, similar to those used to evaluate human learning-independent reasoning. We further studied the mechanisms that support this ability. Our results suggest the possibility of learning-independent abstract reasoning that does not require extensive training.

Naive Few-Shot Learning: Sequence Consistency Evaluation

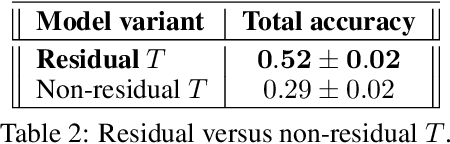
Cognitive psychologists often use the term $\textit{fluid intelligence}$ to describe the ability of humans to solve novel tasks without any prior training. In contrast to humans, deep neural networks can perform cognitive tasks only after extensive (pre-)training with a large number of relevant examples. Motivated by fluid intelligence research in the cognitive sciences, we built a benchmark task which we call sequence consistency evaluation (SCE) that can be used to address this gap. Solving the SCE task requires the ability to extract simple rules from sequences, a basic computation that is required for solving various intelligence tests in humans. We tested $\textit{untrained}$ (naive) deep learning models in the SCE task. Specifically, we compared Relation Networks (RN) and Contrastive Predictive Coding (CPC), two models that can extract simple rules from sequences, and found that the latter, which imposes a structure on the predictable rule does better. We further found that simple networks fare better in this task than complex ones. Finally, we show that this approach can be used for security camera anomaly detection without any prior training.

Naive Artificial Intelligence

In the cognitive sciences, it is common to distinguish between crystal intelligence, the ability to utilize knowledge acquired through past learning or experience and fluid intelligence, the ability to solve novel problems without relying on prior knowledge. Using this cognitive distinction between the two types of intelligence, extensively-trained deep networks that can play chess or Go exhibit crystal but not fluid intelligence. In humans, fluid intelligence is typically studied and quantified using intelligence tests. Previous studies have shown that deep networks can solve some forms of intelligence tests, but only after extensive training. Here we present a computational model that solves intelligence tests without any prior training. This ability is based on continual inductive reasoning, and is implemented by deep unsupervised latent-prediction networks. Our work demonstrates the potential fluid intelligence of deep networks. Finally, we propose that the computational principles underlying our approach can be used to model fluid intelligence in the cognitive sciences.

DORA The Explorer: Directed Outreaching Reinforcement Action-Selection

Exploration is a fundamental aspect of Reinforcement Learning, typically implemented using stochastic action-selection. Exploration, however, can be more efficient if directed toward gaining new world knowledge. Visit-counters have been proven useful both in practice and in theory for directed exploration. However, a major limitation of counters is their locality. While there are a few model-based solutions to this shortcoming, a model-free approach is still missing. We propose $E$-values, a generalization of counters that can be used to evaluate the propagating exploratory value over state-action trajectories. We compare our approach to commonly used RL techniques, and show that using $E$-values improves learning and performance over traditional counters. We also show how our method can be implemented with function approximation to efficiently learn continuous MDPs. We demonstrate this by showing that our approach surpasses state of the art performance in the Freeway Atari 2600 game.