Order parameters and phase transitions of continual learning in deep neural networks

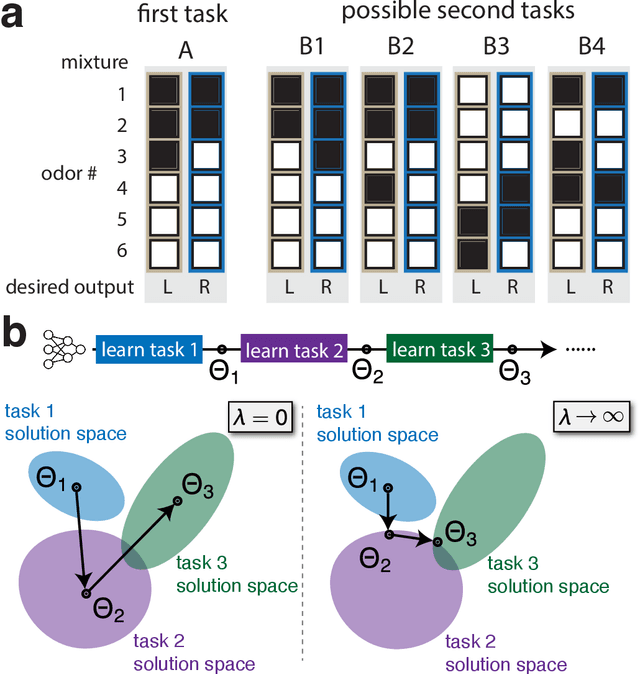
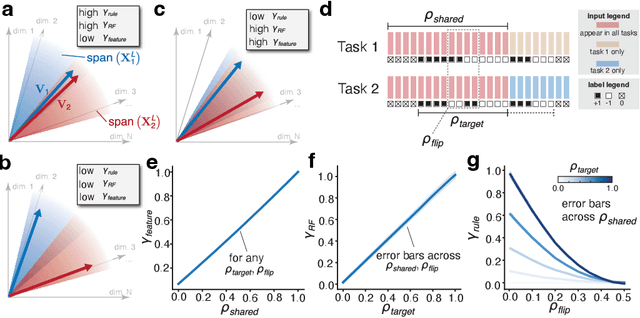
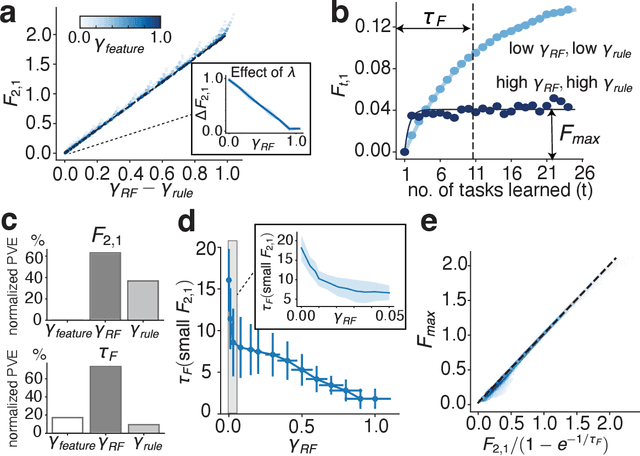
Continual learning (CL) enables animals to learn new tasks without erasing prior knowledge. CL in artificial neural networks (NNs) is challenging due to catastrophic forgetting, where new learning degrades performance on older tasks. While various techniques exist to mitigate forgetting, theoretical insights into when and why CL fails in NNs are lacking. Here, we present a statistical-mechanics theory of CL in deep, wide NNs, which characterizes the network's input-output mapping as it learns a sequence of tasks. It gives rise to order parameters (OPs) that capture how task relations and network architecture influence forgetting and knowledge transfer, as verified by numerical evaluations. We found that the input and rule similarity between tasks have different effects on CL performance. In addition, the theory predicts that increasing the network depth can effectively reduce overlap between tasks, thereby lowering forgetting. For networks with task-specific readouts, the theory identifies a phase transition where CL performance shifts dramatically as tasks become less similar, as measured by the OPs. Sufficiently low similarity leads to catastrophic anterograde interference, where the network retains old tasks perfectly but completely fails to generalize new learning. Our results delineate important factors affecting CL performance and suggest strategies for mitigating forgetting.

Connecting NTK and NNGP: A Unified Theoretical Framework for Neural Network Learning Dynamics in the Kernel Regime

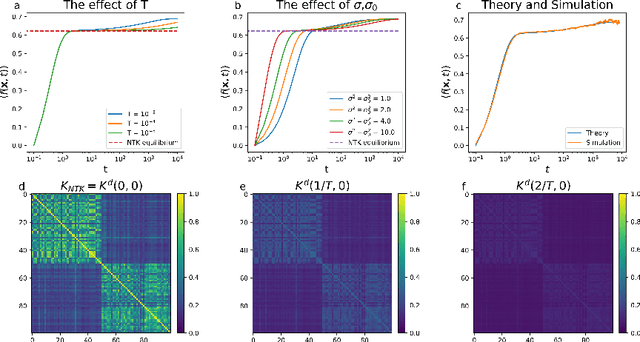
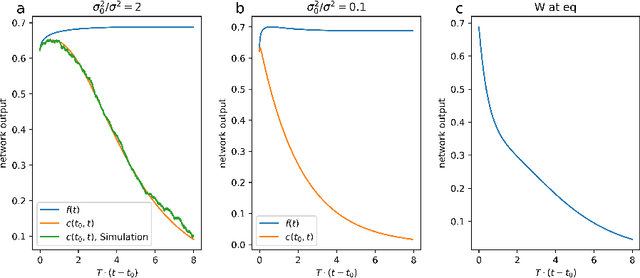
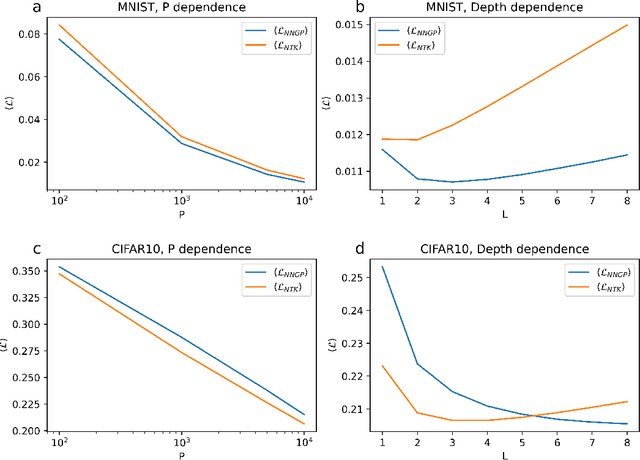
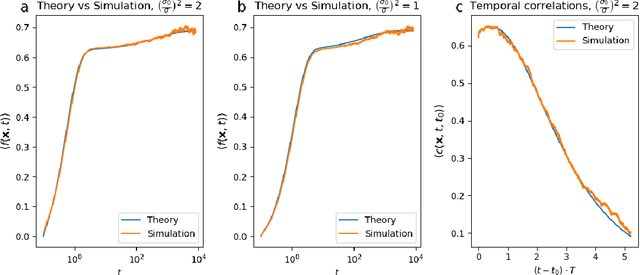
Artificial neural networks have revolutionized machine learning in recent years, but a complete theoretical framework for their learning process is still lacking. Substantial progress has been made for infinitely wide networks. In this regime, two disparate theoretical frameworks have been used, in which the network's output is described using kernels: one framework is based on the Neural Tangent Kernel (NTK) which assumes linearized gradient descent dynamics, while the Neural Network Gaussian Process (NNGP) kernel assumes a Bayesian framework. However, the relation between these two frameworks has remained elusive. This work unifies these two distinct theories using a Markov proximal learning model for learning dynamics in an ensemble of randomly initialized infinitely wide deep networks. We derive an exact analytical expression for the network input-output function during and after learning, and introduce a new time-dependent Neural Dynamical Kernel (NDK) from which both NTK and NNGP kernels can be derived. We identify two learning phases characterized by different time scales: gradient-driven and diffusive learning. In the initial gradient-driven learning phase, the dynamics is dominated by deterministic gradient descent, and is described by the NTK theory. This phase is followed by the diffusive learning stage, during which the network parameters sample the solution space, ultimately approaching the equilibrium distribution corresponding to NNGP. Combined with numerical evaluations on synthetic and benchmark datasets, we provide novel insights into the different roles of initialization, regularization, and network depth, as well as phenomena such as early stopping and representational drift. This work closes the gap between the NTK and NNGP theories, providing a comprehensive framework for understanding the learning process of deep neural networks in the infinite width limit.

Globally Gated Deep Linear Networks

Recently proposed Gated Linear Networks present a tractable nonlinear network architecture, and exhibit interesting capabilities such as learning with local error signals and reduced forgetting in sequential learning. In this work, we introduce a novel gating architecture, named Globally Gated Deep Linear Networks (GGDLNs) where gating units are shared among all processing units in each layer, thereby decoupling the architectures of the nonlinear but unlearned gatings and the learned linear processing motifs. We derive exact equations for the generalization properties in these networks in the finite-width thermodynamic limit, defined by $P,N\rightarrow\infty, P/N\sim O(1)$, where P and N are the training sample size and the network width respectively. We find that the statistics of the network predictor can be expressed in terms of kernels that undergo shape renormalization through a data-dependent matrix compared to the GP kernels. Our theory accurately captures the behavior of finite width GGDLNs trained with gradient descent dynamics. We show that kernel shape renormalization gives rise to rich generalization properties w.r.t. network width, depth and L2 regularization amplitude. Interestingly, networks with sufficient gating units behave similarly to standard ReLU networks. Although gatings in the model do not participate in supervised learning, we show the utility of unsupervised learning of the gating parameters. Additionally, our theory allows the evaluation of the network's ability for learning multiple tasks by incorporating task-relevant information into the gating units. In summary, our work is the first exact theoretical solution of learning in a family of nonlinear networks with finite width. The rich and diverse behavior of the GGDLNs suggests that they are helpful analytically tractable models of learning single and multiple tasks, in finite-width nonlinear deep networks.

Statistical Mechanics of Deep Linear Neural Networks: The Back-Propagating Renormalization Group

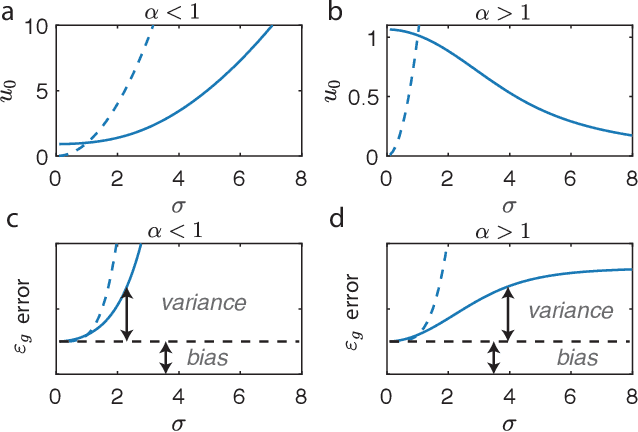
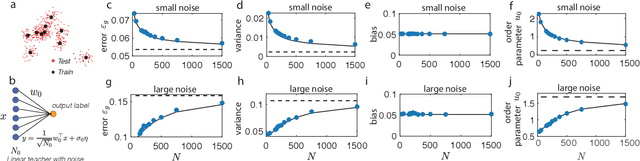
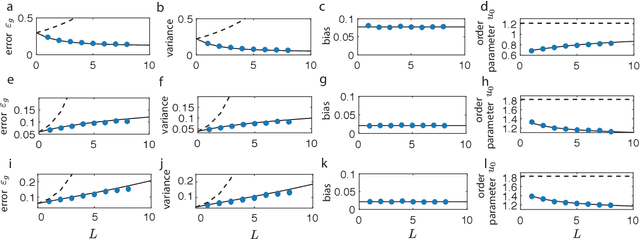
The success of deep learning in many real-world tasks has triggered an effort to theoretically understand the power and limitations of deep learning in training and generalization of complex tasks, so far with limited progress. In this work, we study the statistical mechanics of learning in Deep Linear Neural Networks (DLNNs) in which the input-output function of an individual unit is linear. Despite the linearity of the units, learning in DLNNs is highly nonlinear, hence studying its properties reveals some of the essential features of nonlinear Deep Neural Networks (DNNs). We solve exactly the network properties following supervised learning using an equilibrium Gibbs distribution in the weight space. To do this, we introduce the Back-Propagating Renormalization Group (BPRG) which allows for the incremental integration of the network weights layer by layer from the network output layer and progressing backward. This procedure allows us to evaluate important network properties such as its generalization error, the role of network width and depth, the impact of the size of the training set, and the effects of weight regularization and learning stochasticity. Furthermore, by performing partial integration of layers, BPRG allows us to compute the emergent properties of the neural representations across the different hidden layers. We have proposed a heuristic extension of the BPRG to nonlinear DNNs with rectified linear units (ReLU). Surprisingly, our numerical simulations reveal that despite the nonlinearity, the predictions of our theory are largely shared by ReLU networks with modest depth, in a wide regime of parameters. Our work is the first exact statistical mechanical study of learning in a family of Deep Neural Networks, and the first development of the Renormalization Group approach to the weight space of these systems.