Statistical Mechanics of Deep Linear Neural Networks: The Back-Propagating Renormalization Group

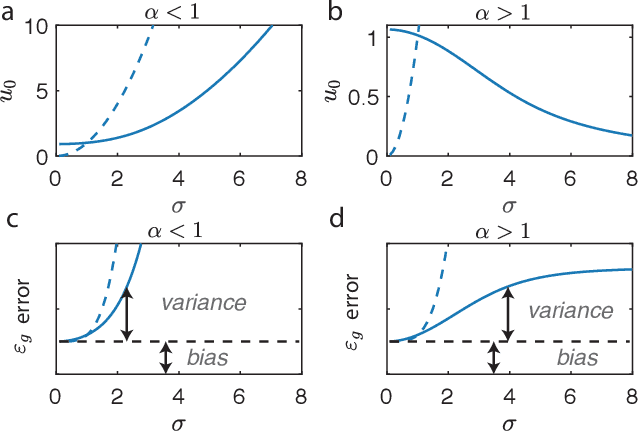
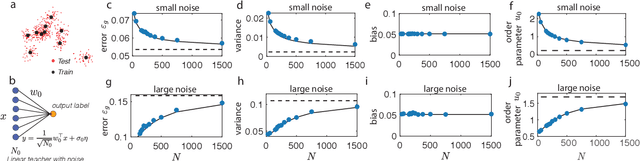
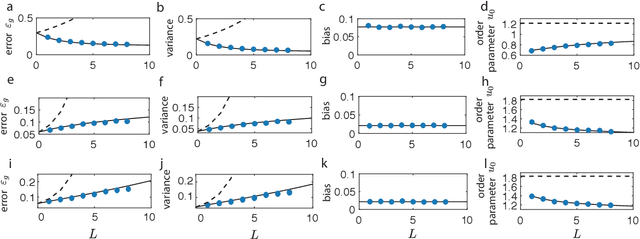
The success of deep learning in many real-world tasks has triggered an effort to theoretically understand the power and limitations of deep learning in training and generalization of complex tasks, so far with limited progress. In this work, we study the statistical mechanics of learning in Deep Linear Neural Networks (DLNNs) in which the input-output function of an individual unit is linear. Despite the linearity of the units, learning in DLNNs is highly nonlinear, hence studying its properties reveals some of the essential features of nonlinear Deep Neural Networks (DNNs). We solve exactly the network properties following supervised learning using an equilibrium Gibbs distribution in the weight space. To do this, we introduce the Back-Propagating Renormalization Group (BPRG) which allows for the incremental integration of the network weights layer by layer from the network output layer and progressing backward. This procedure allows us to evaluate important network properties such as its generalization error, the role of network width and depth, the impact of the size of the training set, and the effects of weight regularization and learning stochasticity. Furthermore, by performing partial integration of layers, BPRG allows us to compute the emergent properties of the neural representations across the different hidden layers. We have proposed a heuristic extension of the BPRG to nonlinear DNNs with rectified linear units (ReLU). Surprisingly, our numerical simulations reveal that despite the nonlinearity, the predictions of our theory are largely shared by ReLU networks with modest depth, in a wide regime of parameters. Our work is the first exact statistical mechanical study of learning in a family of Deep Neural Networks, and the first development of the Renormalization Group approach to the weight space of these systems.