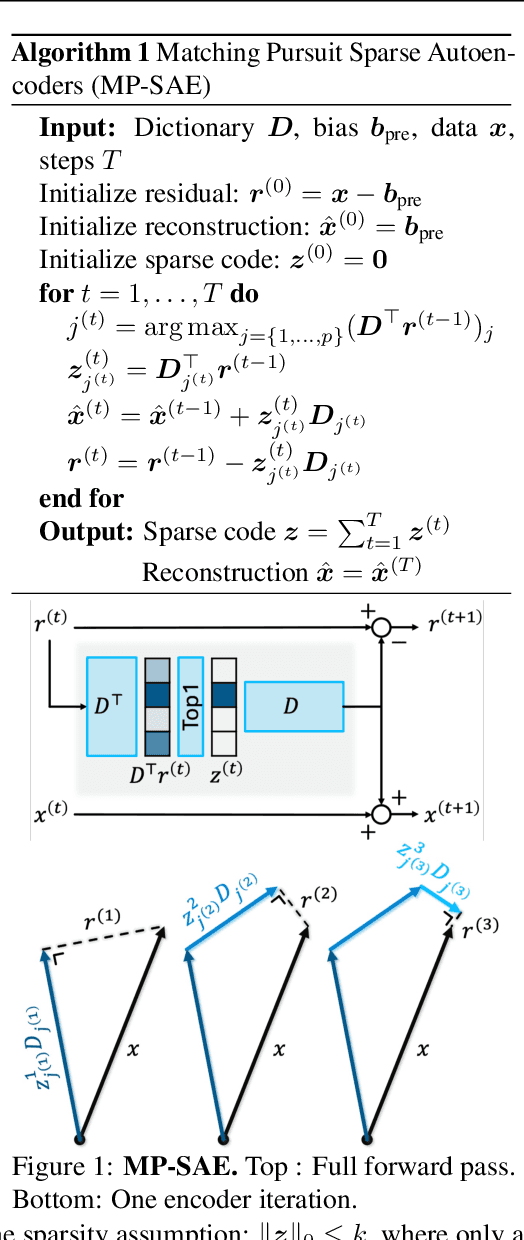
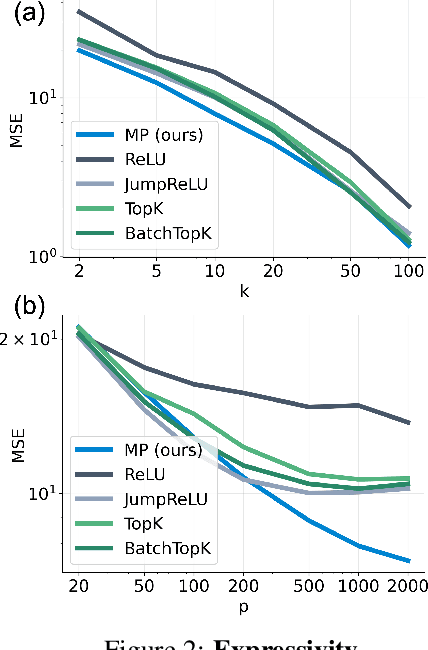
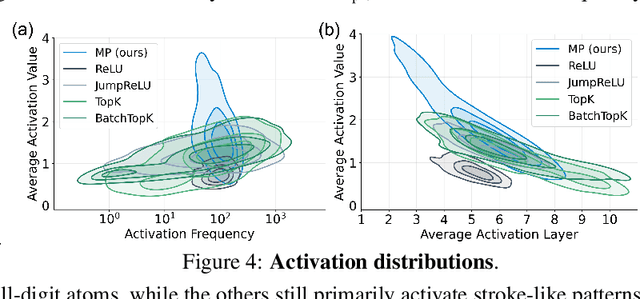
Evaluating Sparse Autoencoders: From Shallow Design to Matching Pursuit

Sparse autoencoders (SAEs) have recently become central tools for interpretability, leveraging dictionary learning principles to extract sparse, interpretable features from neural representations whose underlying structure is typically unknown. This paper evaluates SAEs in a controlled setting using MNIST, which reveals that current shallow architectures implicitly rely on a quasi-orthogonality assumption that limits the ability to extract correlated features. To move beyond this, we introduce a multi-iteration SAE by unrolling Matching Pursuit (MP-SAE), enabling the residual-guided extraction of correlated features that arise in hierarchical settings such as handwritten digit generation while guaranteeing monotonic improvement of the reconstruction as more atoms are selected.

A Decoupled Approach for Composite Sparse-plus-Smooth Penalized Optimization

We consider a linear inverse problem whose solution is expressed as a sum of two components, one of them being smooth while the other presents sparse properties. This problem is solved by minimizing an objective function with a least square data-fidelity term and a different regularization term applied to each of the components. Sparsity is promoted with a $\ell_1$ norm, while the other component is penalized by means of a $\ell_2$ norm. We characterize the solution set of this composite optimization problem by stating a Representer Theorem. Consequently, we identify that solving the optimization problem can be decoupled, first identifying the sparse solution as a solution of a modified single-variable problem, then deducing the smooth component. We illustrate that this decoupled solving method can lead to significant computational speedups in applications, considering the problem of Dirac recovery over a smooth background with two-dimensional partial Fourier measurements.