PolyCLEAN: When Högbom meets Bayes -- Fast Super-Resolution Imaging with Bayesian MAP Estimation

Aims: We address two issues for the adoption of convex optimization in radio interferometric imaging. First, a method for a fine resolution setup is proposed which scales naturally in terms of memory usage and reconstruction speed. Second, a new tool to localize a region of uncertainty is developed, paving the way for quantitative imaging in radio interferometry. Methods: The classical $\ell_1$ penalty is used to turn the inverse problem into a sparsity-promoting optimization. For efficient implementation, the so-called Frank-Wolfe algorithm is used together with a \textit{polyatomic} refinement. The algorithm naturally produces sparse images at each iteration, leveraged to reduce memory and computational requirements. In that regard, PolyCLEAN reproduces the numerical behavior of CLEAN while guaranteeing that it solves the minimization problem of interest. Additionally, we introduce the dual certificate image, which appears as a numerical byproduct of the Frank-Wolfe algorithm. This image is proposed as a tool for uncertainty quantification on the location of the recovered sources. Results: PolyCLEAN demonstrates good scalability performance, in particular for fine-resolution grids. On simulations, the Python-based implementation is competitive with the fast numerically-optimized CLEAN solver. This acceleration does not affect image reconstruction quality: PolyCLEAN images are consistent with CLEAN-obtained ones for both point sources and diffuse emission recovery. We also highlight PolyCLEAN reconstruction capabilities on observed radio measurements. Conclusions: PolyCLEAN can be considered as an alternative to CLEAN in the radio interferometric imaging pipeline, as it enables the use of Bayesian priors without impacting the scalability and numerical performance of the imaging method.

A Decoupled Approach for Composite Sparse-plus-Smooth Penalized Optimization

We consider a linear inverse problem whose solution is expressed as a sum of two components, one of them being smooth while the other presents sparse properties. This problem is solved by minimizing an objective function with a least square data-fidelity term and a different regularization term applied to each of the components. Sparsity is promoted with a $\ell_1$ norm, while the other component is penalized by means of a $\ell_2$ norm. We characterize the solution set of this composite optimization problem by stating a Representer Theorem. Consequently, we identify that solving the optimization problem can be decoupled, first identifying the sparse solution as a solution of a modified single-variable problem, then deducing the smooth component. We illustrate that this decoupled solving method can lead to significant computational speedups in applications, considering the problem of Dirac recovery over a smooth background with two-dimensional partial Fourier measurements.

Une version polyatomique de l'algorithme Frank-Wolfe pour résoudre le problème LASSO en grandes dimensions

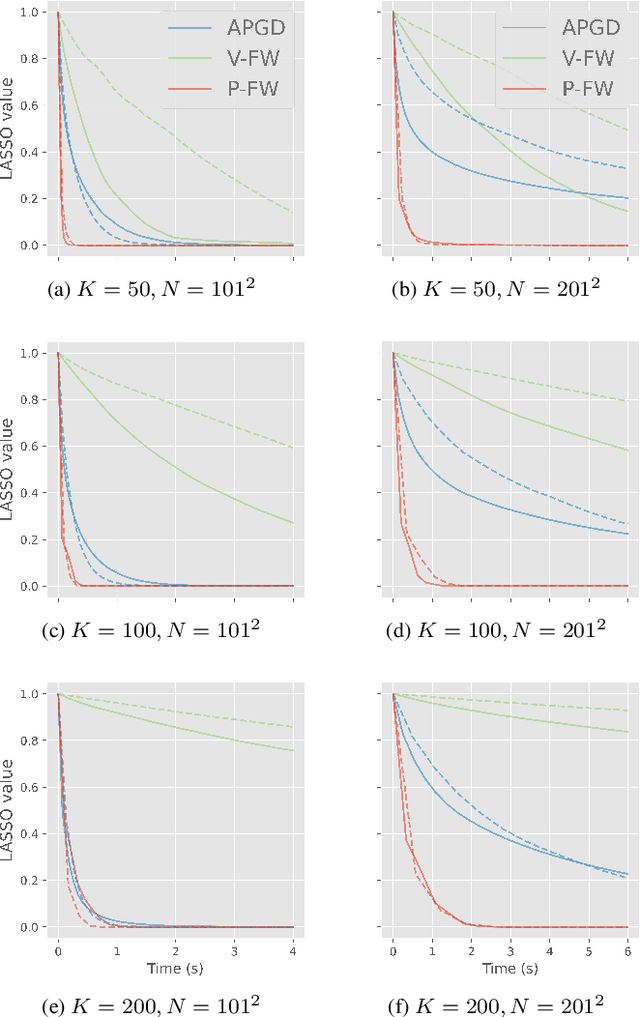
Nous nous int\'eressons \`a la reconstruction parcimonieuse d'images \`a l'aide du probl\`eme d'optimisation r\'egularis\'e LASSO. Dans de nombreuses applications pratiques, les grandes dimensions des objets \`a reconstruire limitent, voire emp\^echent, l'utilisation des m\'ethodes de r\'esolution proximales classiques. C'est le cas par exemple en radioastronomie. Nous d\'etaillons dans cet article le fonctionnement de l'algorithme \textit{Frank-Wolfe Polyatomique}, sp\'ecialement d\'evelopp\'e pour r\'esoudre le probl\`eme LASSO dans ces contextes exigeants. Nous d\'emontrons sa sup\'eriorit\'e par rapport aux m\'ethodes proximales dans des situations en grande dimension avec des mesures de Fourier, lors de la r\'esolution de probl\`emes simul\'es inspir\'es de la radio-interf\'erom\'etrie. -- We consider the problem of recovering sparse images by means of the penalised optimisation problem LASSO. For various practical applications, it is impossible to rely on the proximal solvers commonly used for that purpose due to the size of the objects to recover, as it is the case for radio astronomy. In this article we explain the mechanisms of the \textit{Polyatomic Frank-Wolfe algorithm}, specifically designed to minimise the LASSO problem in such challenging contexts. We demonstrate in simulated problems inspired from radio-interferometry the preeminence of this algorithm over the proximal methods for high dimensional images with Fourier measurements.

A Fast and Scalable Polyatomic Frank-Wolfe Algorithm for the LASSO

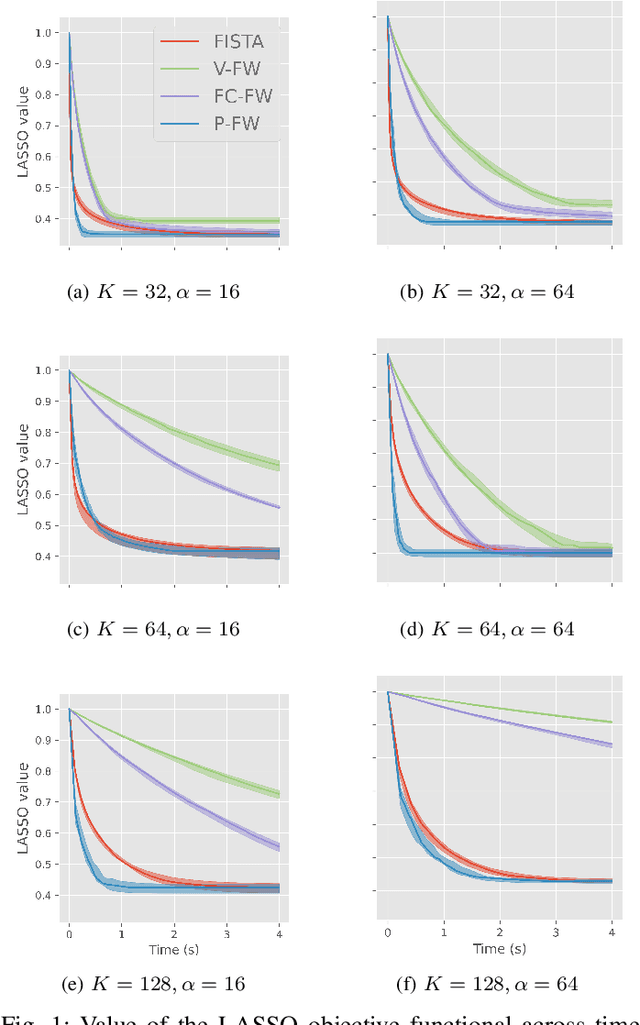
We propose a fast and scalable Polyatomic Frank-Wolfe (P-FW) algorithm for the resolution of high-dimensional LASSO regression problems. The latter improves upon traditional Frank-Wolfe methods by considering generalized greedy steps with polyatomic (i.e. linear combinations of multiple atoms) update directions, hence allowing for a more efficient exploration of the search space. To preserve sparsity of the intermediate iterates, we moreover re-optimize the LASSO problem over the set of selected atoms at each iteration. For efficiency reasons, the accuracy of this re-optimization step is relatively low for early iterations and gradually increases with the iteration count. We provide convergence guarantees for our algorithm and validate it in simulated compressed sensing setups. Our experiments reveal that P-FW outperforms state-of-the-art methods in terms of runtime, both for FW methods and optimal first-order proximal gradient methods such as the Fast Iterative Soft-Thresholding Algorithm (FISTA).

About Graph Degeneracy, Representation Learning and Scalability

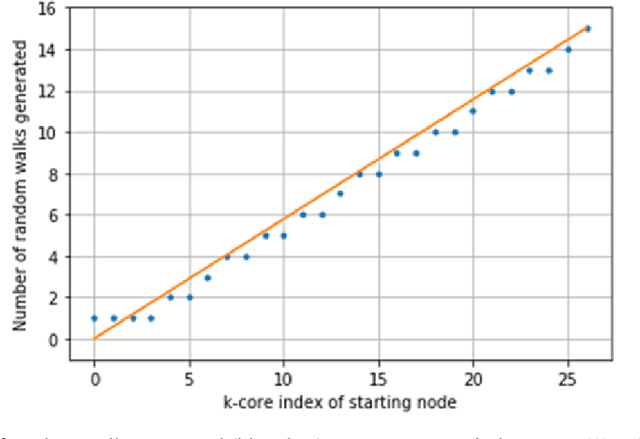
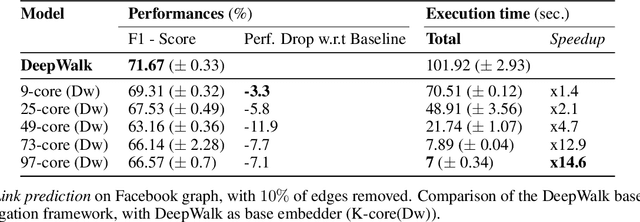
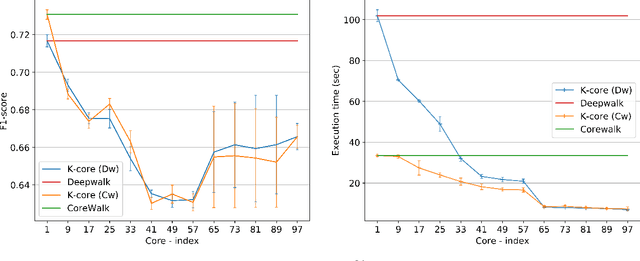
Graphs or networks are a very convenient way to represent data with lots of interaction. Recently, Machine Learning on Graph data has gained a lot of traction. In particular, vertex classification and missing edge detection have very interesting applications, ranging from drug discovery to recommender systems. To achieve such tasks, tremendous work has been accomplished to learn embedding of nodes and edges into finite-dimension vector spaces. This task is called Graph Representation Learning. However, Graph Representation Learning techniques often display prohibitive time and memory complexities, preventing their use in real-time with business size graphs. In this paper, we address this issue by leveraging a degeneracy property of Graphs - the K-Core Decomposition. We present two techniques taking advantage of this decomposition to reduce the time and memory consumption of walk-based Graph Representation Learning algorithms. We evaluate the performances, expressed in terms of quality of embedding and computational resources, of the proposed techniques on several academic datasets. Our code is available at https://github.com/SBrandeis/kcore-embedding