Une version polyatomique de l'algorithme Frank-Wolfe pour résoudre le problème LASSO en grandes dimensions
Paper and Code
Apr 28, 2022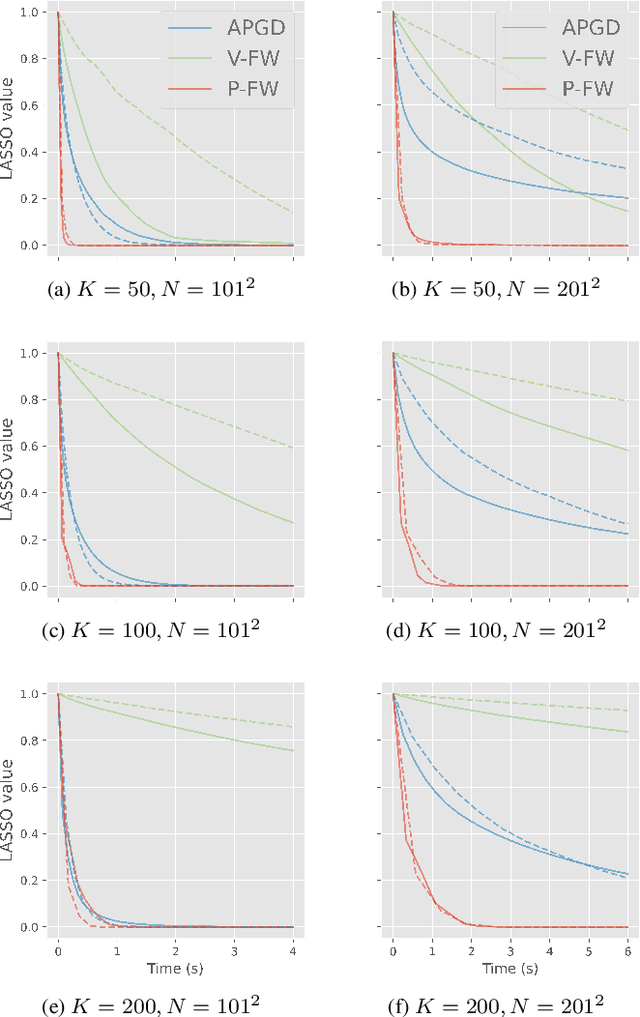
Nous nous int\'eressons \`a la reconstruction parcimonieuse d'images \`a l'aide du probl\`eme d'optimisation r\'egularis\'e LASSO. Dans de nombreuses applications pratiques, les grandes dimensions des objets \`a reconstruire limitent, voire emp\^echent, l'utilisation des m\'ethodes de r\'esolution proximales classiques. C'est le cas par exemple en radioastronomie. Nous d\'etaillons dans cet article le fonctionnement de l'algorithme \textit{Frank-Wolfe Polyatomique}, sp\'ecialement d\'evelopp\'e pour r\'esoudre le probl\`eme LASSO dans ces contextes exigeants. Nous d\'emontrons sa sup\'eriorit\'e par rapport aux m\'ethodes proximales dans des situations en grande dimension avec des mesures de Fourier, lors de la r\'esolution de probl\`emes simul\'es inspir\'es de la radio-interf\'erom\'etrie. -- We consider the problem of recovering sparse images by means of the penalised optimisation problem LASSO. For various practical applications, it is impossible to rely on the proximal solvers commonly used for that purpose due to the size of the objects to recover, as it is the case for radio astronomy. In this article we explain the mechanisms of the \textit{Polyatomic Frank-Wolfe algorithm}, specifically designed to minimise the LASSO problem in such challenging contexts. We demonstrate in simulated problems inspired from radio-interferometry the preeminence of this algorithm over the proximal methods for high dimensional images with Fourier measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge