PolyCLEAN: When Högbom meets Bayes -- Fast Super-Resolution Imaging with Bayesian MAP Estimation

Aims: We address two issues for the adoption of convex optimization in radio interferometric imaging. First, a method for a fine resolution setup is proposed which scales naturally in terms of memory usage and reconstruction speed. Second, a new tool to localize a region of uncertainty is developed, paving the way for quantitative imaging in radio interferometry. Methods: The classical $\ell_1$ penalty is used to turn the inverse problem into a sparsity-promoting optimization. For efficient implementation, the so-called Frank-Wolfe algorithm is used together with a \textit{polyatomic} refinement. The algorithm naturally produces sparse images at each iteration, leveraged to reduce memory and computational requirements. In that regard, PolyCLEAN reproduces the numerical behavior of CLEAN while guaranteeing that it solves the minimization problem of interest. Additionally, we introduce the dual certificate image, which appears as a numerical byproduct of the Frank-Wolfe algorithm. This image is proposed as a tool for uncertainty quantification on the location of the recovered sources. Results: PolyCLEAN demonstrates good scalability performance, in particular for fine-resolution grids. On simulations, the Python-based implementation is competitive with the fast numerically-optimized CLEAN solver. This acceleration does not affect image reconstruction quality: PolyCLEAN images are consistent with CLEAN-obtained ones for both point sources and diffuse emission recovery. We also highlight PolyCLEAN reconstruction capabilities on observed radio measurements. Conclusions: PolyCLEAN can be considered as an alternative to CLEAN in the radio interferometric imaging pipeline, as it enables the use of Bayesian priors without impacting the scalability and numerical performance of the imaging method.

A Decoupled Approach for Composite Sparse-plus-Smooth Penalized Optimization

We consider a linear inverse problem whose solution is expressed as a sum of two components, one of them being smooth while the other presents sparse properties. This problem is solved by minimizing an objective function with a least square data-fidelity term and a different regularization term applied to each of the components. Sparsity is promoted with a $\ell_1$ norm, while the other component is penalized by means of a $\ell_2$ norm. We characterize the solution set of this composite optimization problem by stating a Representer Theorem. Consequently, we identify that solving the optimization problem can be decoupled, first identifying the sparse solution as a solution of a modified single-variable problem, then deducing the smooth component. We illustrate that this decoupled solving method can lead to significant computational speedups in applications, considering the problem of Dirac recovery over a smooth background with two-dimensional partial Fourier measurements.

Une version polyatomique de l'algorithme Frank-Wolfe pour résoudre le problème LASSO en grandes dimensions

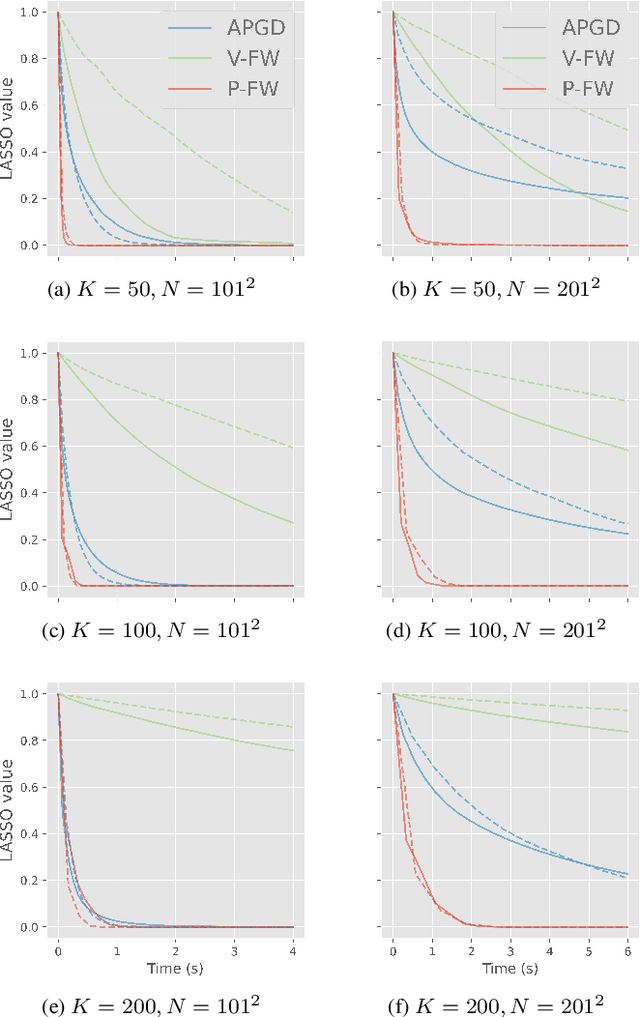
Nous nous int\'eressons \`a la reconstruction parcimonieuse d'images \`a l'aide du probl\`eme d'optimisation r\'egularis\'e LASSO. Dans de nombreuses applications pratiques, les grandes dimensions des objets \`a reconstruire limitent, voire emp\^echent, l'utilisation des m\'ethodes de r\'esolution proximales classiques. C'est le cas par exemple en radioastronomie. Nous d\'etaillons dans cet article le fonctionnement de l'algorithme \textit{Frank-Wolfe Polyatomique}, sp\'ecialement d\'evelopp\'e pour r\'esoudre le probl\`eme LASSO dans ces contextes exigeants. Nous d\'emontrons sa sup\'eriorit\'e par rapport aux m\'ethodes proximales dans des situations en grande dimension avec des mesures de Fourier, lors de la r\'esolution de probl\`emes simul\'es inspir\'es de la radio-interf\'erom\'etrie. -- We consider the problem of recovering sparse images by means of the penalised optimisation problem LASSO. For various practical applications, it is impossible to rely on the proximal solvers commonly used for that purpose due to the size of the objects to recover, as it is the case for radio astronomy. In this article we explain the mechanisms of the \textit{Polyatomic Frank-Wolfe algorithm}, specifically designed to minimise the LASSO problem in such challenging contexts. We demonstrate in simulated problems inspired from radio-interferometry the preeminence of this algorithm over the proximal methods for high dimensional images with Fourier measurements.

TV-based Spline Reconstruction with Fourier Measurements: Uniqueness and Convergence of Grid-Based Methods

We study the problem of recovering piecewise-polynomial periodic functions from their low-frequency information. This means that we only have access to possibly corrupted versions of the Fourier samples of the ground truth up to a maximum cutoff frequency $K_c$. The reconstruction task is specified as an optimization problem with total-variation (TV) regularization (in the sense of measures) involving the $M$-th order derivative regularization operator $\mathrm{L} = \mathrm{D}^M$. The order $M \geq 1$ determines the degree of the reconstructed piecewise polynomial spline, whereas the TV regularization norm, which is known to promote sparsity, guarantees a small number of pieces. We show that the solution of our optimization problem is always unique, which, to the best of our knowledge, is a first for TV-based problems. Moreover, we show that this solution is a periodic spline matched to the regularization operator $\mathrm{L}$ whose number of knots is upper-bounded by $2 K_c$. We then consider the grid-based discretization of our optimization problem in the space of uniform $\mathrm{L}$-splines. On the theoretical side, we show that any sequence of solutions of the discretized problem converges uniformly to the unique solution of the gridless problem as the grid size vanishes. Finally, on the algorithmic side, we propose a B-spline-based algorithm to solve the grid-based problem, and we demonstrate its numerical feasibility experimentally. On both of these aspects, we leverage the uniqueness of the solution of the original problem.

A Fast and Scalable Polyatomic Frank-Wolfe Algorithm for the LASSO

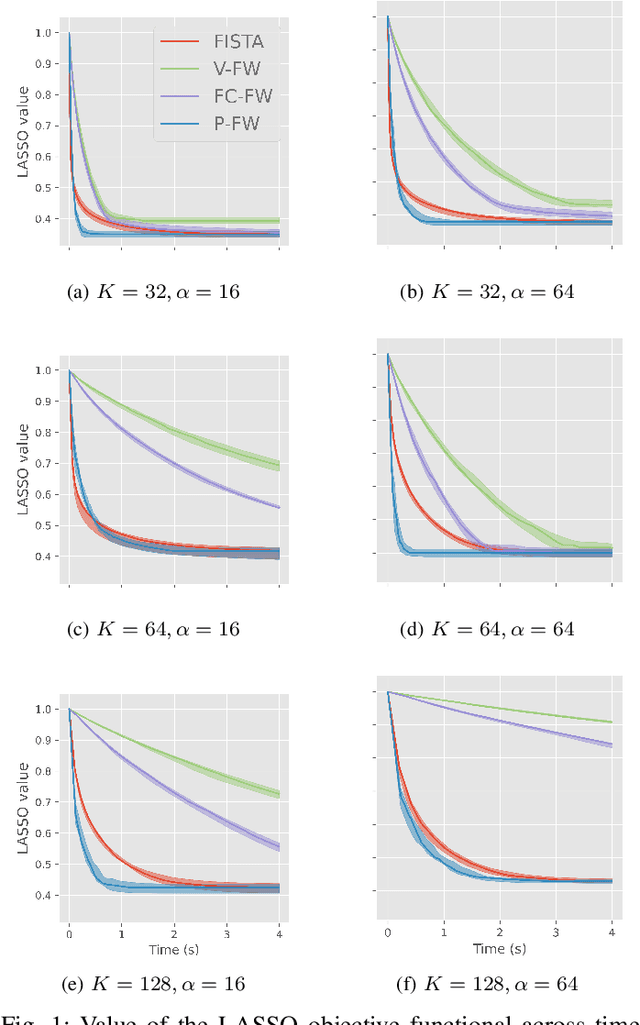
We propose a fast and scalable Polyatomic Frank-Wolfe (P-FW) algorithm for the resolution of high-dimensional LASSO regression problems. The latter improves upon traditional Frank-Wolfe methods by considering generalized greedy steps with polyatomic (i.e. linear combinations of multiple atoms) update directions, hence allowing for a more efficient exploration of the search space. To preserve sparsity of the intermediate iterates, we moreover re-optimize the LASSO problem over the set of selected atoms at each iteration. For efficiency reasons, the accuracy of this re-optimization step is relatively low for early iterations and gradually increases with the iteration count. We provide convergence guarantees for our algorithm and validate it in simulated compressed sensing setups. Our experiments reveal that P-FW outperforms state-of-the-art methods in terms of runtime, both for FW methods and optimal first-order proximal gradient methods such as the Fast Iterative Soft-Thresholding Algorithm (FISTA).

3D Solid Spherical Bispectrum CNNs for Biomedical Texture Analysis

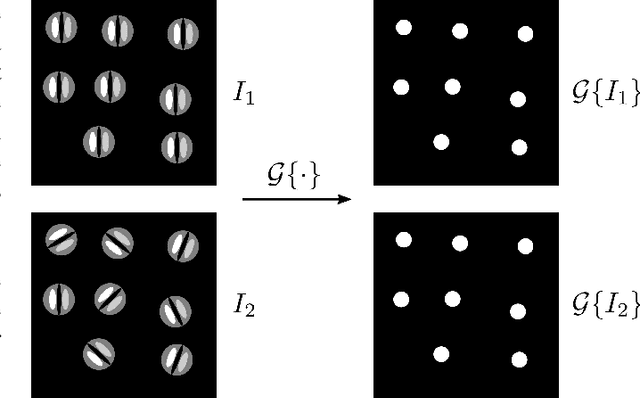
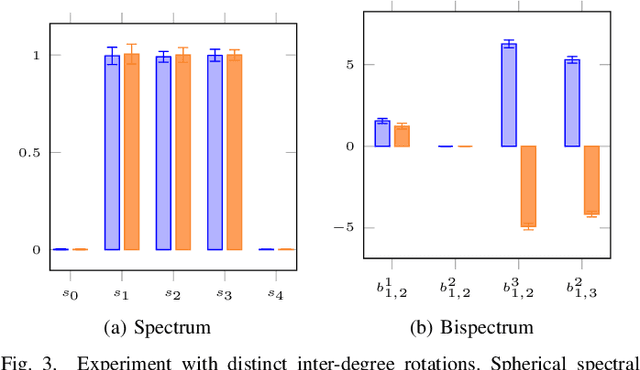
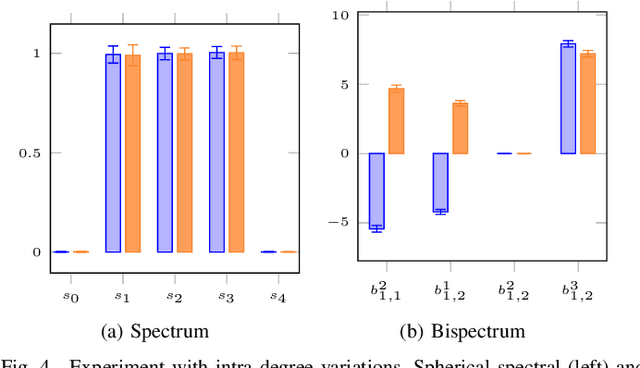
Locally Rotation Invariant (LRI) operators have shown great potential in biomedical texture analysis where patterns appear at random positions and orientations. LRI operators can be obtained by computing the responses to the discrete rotation of local descriptors, such as Local Binary Patterns (LBP) or the Scale Invariant Feature Transform (SIFT). Other strategies achieve this invariance using Laplacian of Gaussian or steerable wavelets for instance, preventing the introduction of sampling errors during the discretization of the rotations. In this work, we obtain LRI operators via the local projection of the image on the spherical harmonics basis, followed by the computation of the bispectrum, which shares and extends the invariance properties of the spectrum. We investigate the benefits of using the bispectrum over the spectrum in the design of a LRI layer embedded in a shallow Convolutional Neural Network (CNN) for 3D image analysis. The performance of each design is evaluated on two datasets and compared against a standard 3D CNN. The first dataset is made of 3D volumes composed of synthetically generated rotated patterns, while the second contains malignant and benign pulmonary nodules in Computed Tomography (CT) images. The results indicate that bispectrum CNNs allows for a significantly better characterization of 3D textures than both the spectral and standard CNN. In addition, it can efficiently learn with fewer training examples and trainable parameters when compared to a standard convolutional layer.

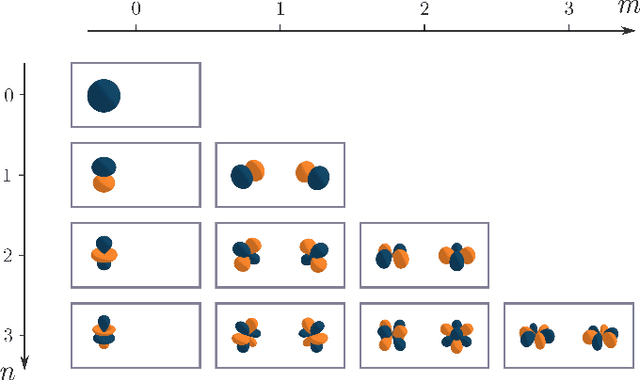
Local Rotation Invariance in 3D CNNs

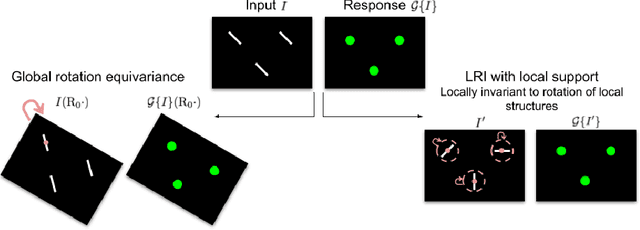
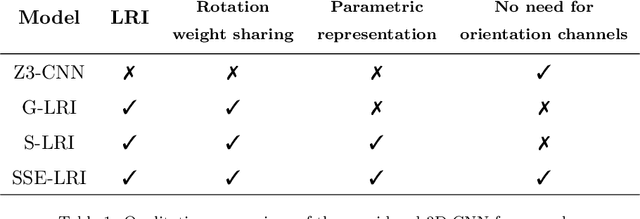
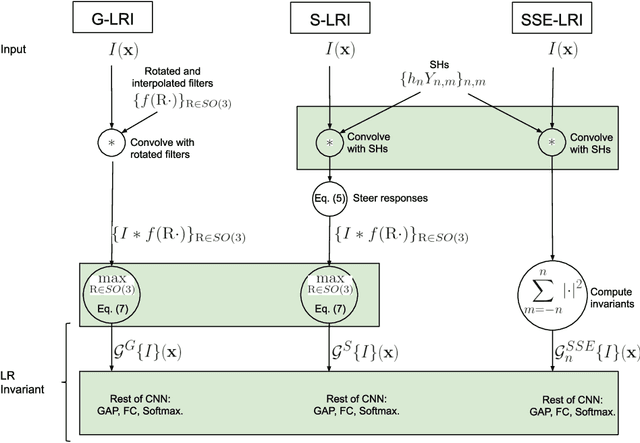
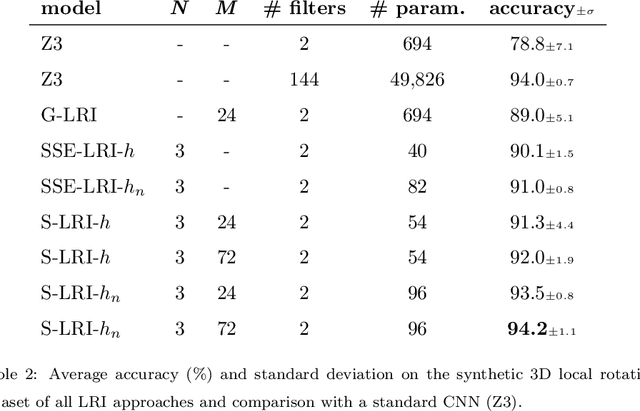
Locally Rotation Invariant (LRI) image analysis was shown to be fundamental in many applications and in particular in medical imaging where local structures of tissues occur at arbitrary rotations. LRI constituted the cornerstone of several breakthroughs in texture analysis, including Local Binary Patterns (LBP), Maximum Response 8 (MR8) and steerable filterbanks. Whereas globally rotation invariant Convolutional Neural Networks (CNN) were recently proposed, LRI was very little investigated in the context of deep learning. LRI designs allow learning filters accounting for all orientations, which enables a drastic reduction of trainable parameters and training data when compared to standard 3D CNNs. In this paper, we propose and compare several methods to obtain LRI CNNs with directional sensitivity. Two methods use orientation channels (responses to rotated kernels), either by explicitly rotating the kernels or using steerable filters. These orientation channels constitute a locally rotation equivariant representation of the data. Local pooling across orientations yields LRI image analysis. Steerable filters are used to achieve a fine and efficient sampling of 3D rotations as well as a reduction of trainable parameters and operations, thanks to a parametric representations involving solid Spherical Harmonics (SH), which are products of SH with associated learned radial profiles.Finally, we investigate a third strategy to obtain LRI based on rotational invariants calculated from responses to a learned set of solid SHs. The proposed methods are evaluated and compared to standard CNNs on 3D datasets including synthetic textured volumes composed of rotated patterns, and pulmonary nodule classification in CT. The results show the importance of LRI image analysis while resulting in a drastic reduction of trainable parameters, outperforming standard 3D CNNs trained with data augmentation.

Native Banach spaces for splines and variational inverse problems

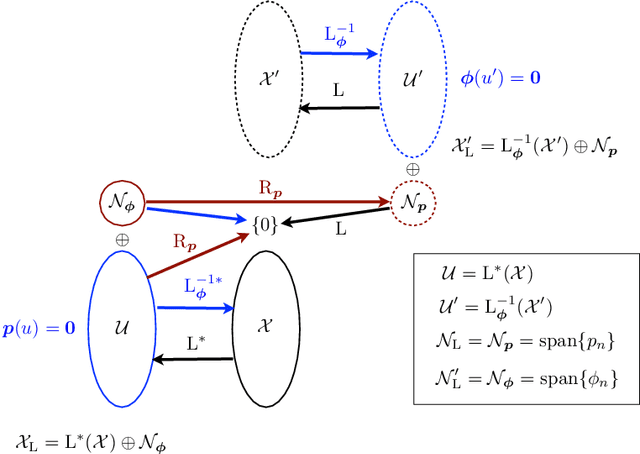
We propose a systematic construction of native Banach spaces for general spline-admissible operators ${\rm L}$. In short, the native space for ${\rm L}$ and the (dual) norm $\|\cdot\|_{\mathcal{X}'}$ is the largest space of functions $f: \mathbb{R}^d \to \mathbb{R}$ such that $\|{\rm L} f\|_{\mathcal{X}'}<\infty$, subject to the constraint that the growth-restricted null space of ${\rm L}$be finite-dimensional. This space, denoted by $\mathcal{X}'_{\rm L}$, is specified as the dual of the pre-native space $\mathcal{X}_{\rm L}$, which is itself obtained through a suitable completion process. The main difference with prior constructions (e.g., reproducing kernel Hilbert spaces) is that our approach involves test functions rather than sums of atoms (e.g, kernels), which makes it applicable to a much broader class of norms, including total variation. Under specific admissibility and compatibility hypotheses, we lay out the direct-sum topology of $\mathcal{X}_{\rm L}$ and $\mathcal{X}'_{\rm L}$, and identify the whole family of equivalent norms. Our construction ensures that the native space and its pre-dual are endowed with a fundamental Schwartz-Banach property. In practical terms, this means that $\mathcal{X}'_{\rm L}$ is rich enough to reproduce any function with an arbitrary degree of precision.