Native Banach spaces for splines and variational inverse problems
Paper and Code
Apr 24, 2019
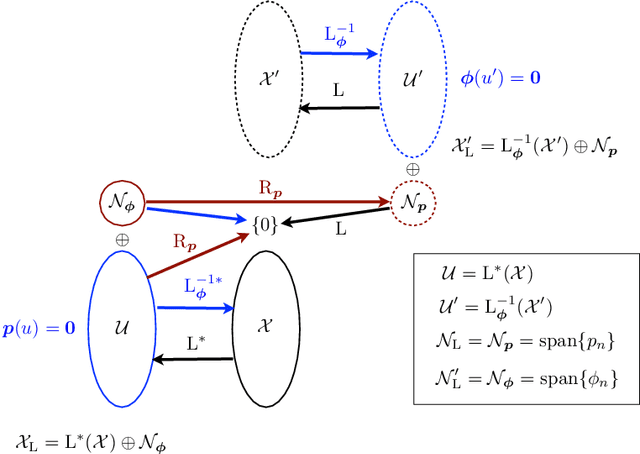
We propose a systematic construction of native Banach spaces for general spline-admissible operators ${\rm L}$. In short, the native space for ${\rm L}$ and the (dual) norm $\|\cdot\|_{\mathcal{X}'}$ is the largest space of functions $f: \mathbb{R}^d \to \mathbb{R}$ such that $\|{\rm L} f\|_{\mathcal{X}'}<\infty$, subject to the constraint that the growth-restricted null space of ${\rm L}$be finite-dimensional. This space, denoted by $\mathcal{X}'_{\rm L}$, is specified as the dual of the pre-native space $\mathcal{X}_{\rm L}$, which is itself obtained through a suitable completion process. The main difference with prior constructions (e.g., reproducing kernel Hilbert spaces) is that our approach involves test functions rather than sums of atoms (e.g, kernels), which makes it applicable to a much broader class of norms, including total variation. Under specific admissibility and compatibility hypotheses, we lay out the direct-sum topology of $\mathcal{X}_{\rm L}$ and $\mathcal{X}'_{\rm L}$, and identify the whole family of equivalent norms. Our construction ensures that the native space and its pre-dual are endowed with a fundamental Schwartz-Banach property. In practical terms, this means that $\mathcal{X}'_{\rm L}$ is rich enough to reproduce any function with an arbitrary degree of precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge