PolyCLEAN: When Högbom meets Bayes -- Fast Super-Resolution Imaging with Bayesian MAP Estimation

Aims: We address two issues for the adoption of convex optimization in radio interferometric imaging. First, a method for a fine resolution setup is proposed which scales naturally in terms of memory usage and reconstruction speed. Second, a new tool to localize a region of uncertainty is developed, paving the way for quantitative imaging in radio interferometry. Methods: The classical $\ell_1$ penalty is used to turn the inverse problem into a sparsity-promoting optimization. For efficient implementation, the so-called Frank-Wolfe algorithm is used together with a \textit{polyatomic} refinement. The algorithm naturally produces sparse images at each iteration, leveraged to reduce memory and computational requirements. In that regard, PolyCLEAN reproduces the numerical behavior of CLEAN while guaranteeing that it solves the minimization problem of interest. Additionally, we introduce the dual certificate image, which appears as a numerical byproduct of the Frank-Wolfe algorithm. This image is proposed as a tool for uncertainty quantification on the location of the recovered sources. Results: PolyCLEAN demonstrates good scalability performance, in particular for fine-resolution grids. On simulations, the Python-based implementation is competitive with the fast numerically-optimized CLEAN solver. This acceleration does not affect image reconstruction quality: PolyCLEAN images are consistent with CLEAN-obtained ones for both point sources and diffuse emission recovery. We also highlight PolyCLEAN reconstruction capabilities on observed radio measurements. Conclusions: PolyCLEAN can be considered as an alternative to CLEAN in the radio interferometric imaging pipeline, as it enables the use of Bayesian priors without impacting the scalability and numerical performance of the imaging method.

pyFFS: A Python Library for Fast Fourier Series Computation

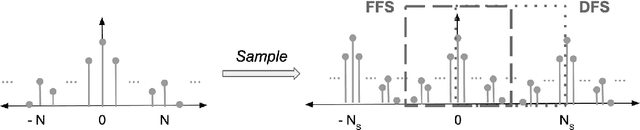
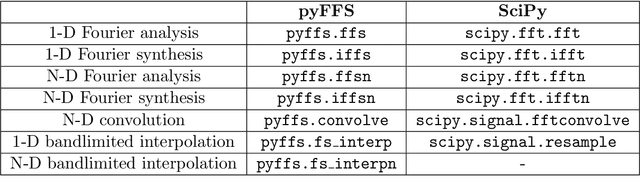
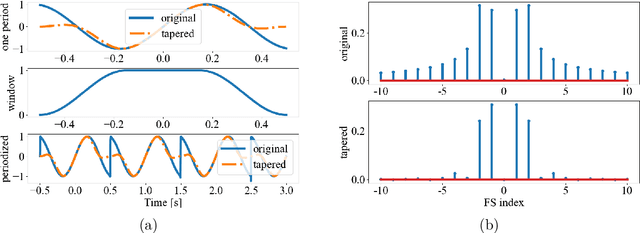
Fourier transforms are an often necessary component in many computational tasks, and can be computed efficiently through the fast Fourier transform (FFT) algorithm. However, many applications involve an underlying continuous signal, and a more natural choice would be to work with e.g. the Fourier series (FS) coefficients in order to avoid the additional overhead of translating between the analog and discrete domains. Unfortunately, there exists very little literature and tools for the manipulation of FS coefficients from discrete samples. This paper introduces a Python library called pyFFS for efficient FS coefficient computation, convolution, and interpolation. While the libraries SciPy and NumPy provide efficient functionality for discrete Fourier transform coefficients via the FFT algorithm, pyFFS addresses the computation of FS coefficients through what we call the fast Fourier series (FFS). Moreover, pyFFS includes an FS interpolation method based on the chirp Z-transform that can make it more than an order of magnitude faster than the SciPy equivalent when one wishes to perform interpolation. GPU support through the CuPy library allows for further acceleration, e.g. an order of magnitude faster for computing the 2-D FS coefficients of 1000 x 1000 samples and nearly two orders of magnitude faster for 2-D interpolation. As an application, we discuss the use of pyFFS in Fourier optics. pyFFS is available as an open source package at https://github.com/imagingofthings/pyFFS, with documentation at https://pyffs.readthedocs.io.