An Efficient Algorithm for Clustered Multi-Task Compressive Sensing

This paper considers clustered multi-task compressive sensing, a hierarchical model that solves multiple compressive sensing tasks by finding clusters of tasks that leverage shared information to mutually improve signal reconstruction. The existing inference algorithm for this model is computationally expensive and does not scale well in high dimensions. The main bottleneck involves repeated matrix inversion and log-determinant computation for multiple large covariance matrices. We propose a new algorithm that substantially accelerates model inference by avoiding the need to explicitly compute these covariance matrices. Our approach combines Monte Carlo sampling with iterative linear solvers. Our experiments reveal that compared to the existing baseline, our algorithm can be up to thousands of times faster and an order of magnitude more memory-efficient.

Probabilistic Unrolling: Scalable, Inverse-Free Maximum Likelihood Estimation for Latent Gaussian Models

Latent Gaussian models have a rich history in statistics and machine learning, with applications ranging from factor analysis to compressed sensing to time series analysis. The classical method for maximizing the likelihood of these models is the expectation-maximization (EM) algorithm. For problems with high-dimensional latent variables and large datasets, EM scales poorly because it needs to invert as many large covariance matrices as the number of data points. We introduce probabilistic unrolling, a method that combines Monte Carlo sampling with iterative linear solvers to circumvent matrix inversion. Our theoretical analyses reveal that unrolling and backpropagation through the iterations of the solver can accelerate gradient estimation for maximum likelihood estimation. In experiments on simulated and real data, we demonstrate that probabilistic unrolling learns latent Gaussian models up to an order of magnitude faster than gradient EM, with minimal losses in model performance.

Word-Level Explanations for Analyzing Bias in Text-to-Image Models

Text-to-image models take a sentence (i.e., prompt) and generate images associated with this input prompt. These models have created award wining-art, videos, and even synthetic datasets. However, text-to-image (T2I) models can generate images that underrepresent minorities based on race and sex. This paper investigates which word in the input prompt is responsible for bias in generated images. We introduce a method for computing scores for each word in the prompt; these scores represent its influence on biases in the model's output. Our method follows the principle of \emph{explaining by removing}, leveraging masked language models to calculate the influence scores. We perform experiments on Stable Diffusion to demonstrate that our method identifies the replication of societal stereotypes in generated images.

High-Dimensional Sparse Bayesian Learning without Covariance Matrices

Sparse Bayesian learning (SBL) is a powerful framework for tackling the sparse coding problem. However, the most popular inference algorithms for SBL become too expensive for high-dimensional settings, due to the need to store and compute a large covariance matrix. We introduce a new inference scheme that avoids explicit construction of the covariance matrix by solving multiple linear systems in parallel to obtain the posterior moments for SBL. Our approach couples a little-known diagonal estimation result from numerical linear algebra with the conjugate gradient algorithm. On several simulations, our method scales better than existing approaches in computation time and memory, especially for structured dictionaries capable of fast matrix-vector multiplication.

Mixture Model Auto-Encoders: Deep Clustering through Dictionary Learning

State-of-the-art approaches for clustering high-dimensional data utilize deep auto-encoder architectures. Many of these networks require a large number of parameters and suffer from a lack of interpretability, due to the black-box nature of the auto-encoders. We introduce Mixture Model Auto-Encoders (MixMate), a novel architecture that clusters data by performing inference on a generative model. Derived from the perspective of sparse dictionary learning and mixture models, MixMate comprises several auto-encoders, each tasked with reconstructing data in a distinct cluster, while enforcing sparsity in the latent space. Through experiments on various image datasets, we show that MixMate achieves competitive performance compared to state-of-the-art deep clustering algorithms, while using orders of magnitude fewer parameters.

Covariance-Free Sparse Bayesian Learning

Sparse Bayesian learning (SBL) is a powerful framework for tackling the sparse coding problem while also providing uncertainty quantification. However, the most popular inference algorithms for SBL become too expensive for high-dimensional problems due to the need to maintain a large covariance matrix. To resolve this issue, we introduce a new SBL inference algorithm that avoids explicit computation of the covariance matrix, thereby saving significant time and space. Instead of performing costly matrix inversions, our covariance-free method solves multiple linear systems to obtain provably unbiased estimates of the posterior statistics needed by SBL. These systems can be solved in parallel, enabling further acceleration of the algorithm via graphics processing units. In practice, our method can be up to thousands of times faster than existing baselines, reducing hours of computation time to seconds. We showcase how our new algorithm enables SBL to tractably tackle high-dimensional signal recovery problems, such as deconvolution of calcium imaging data and multi-contrast reconstruction of magnetic resonance images. Finally, we open-source a toolbox containing all of our implementations to drive future research in SBL.

Autoregressive Knowledge Distillation through Imitation Learning

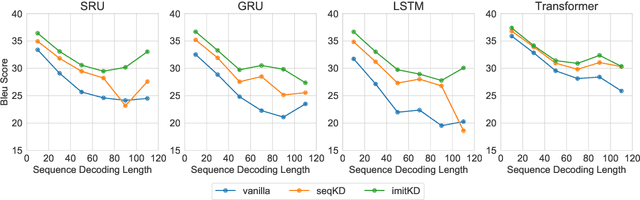
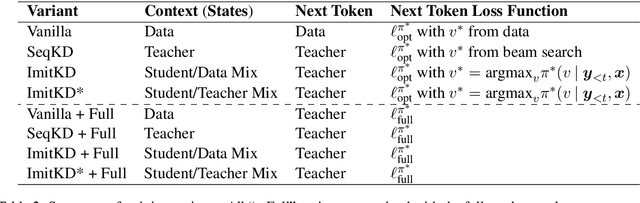
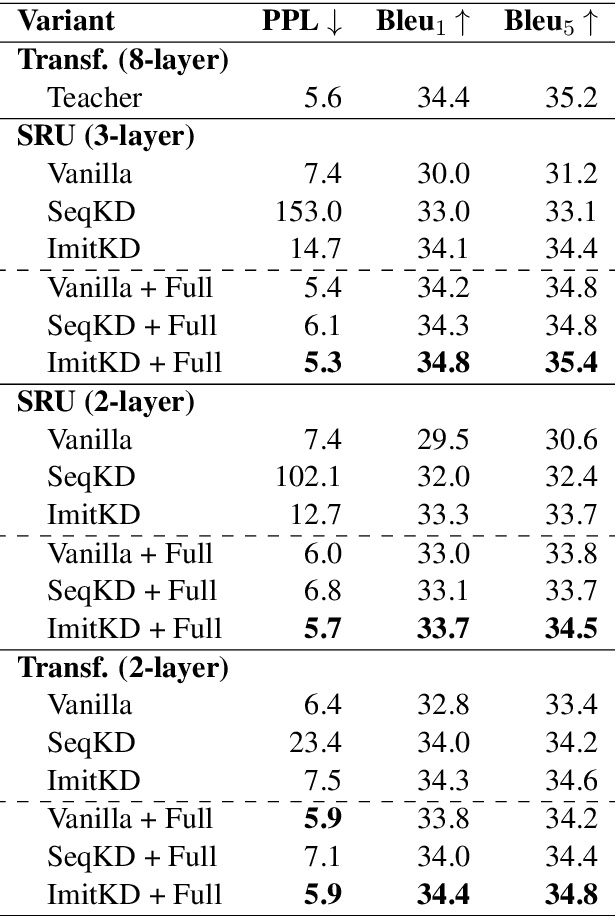
The performance of autoregressive models on natural language generation tasks has dramatically improved due to the adoption of deep, self-attentive architectures. However, these gains have come at the cost of hindering inference speed, making state-of-the-art models cumbersome to deploy in real-world, time-sensitive settings. We develop a compression technique for autoregressive models that is driven by an imitation learning perspective on knowledge distillation. The algorithm is designed to address the exposure bias problem. On prototypical language generation tasks such as translation and summarization, our method consistently outperforms other distillation algorithms, such as sequence-level knowledge distillation. Student models trained with our method attain 1.4 to 4.8 BLEU/ROUGE points higher than those trained from scratch, while increasing inference speed by up to 14 times in comparison to the teacher model.

Clustering Time Series with Nonlinear Dynamics: A Bayesian Non-Parametric and Particle-Based Approach

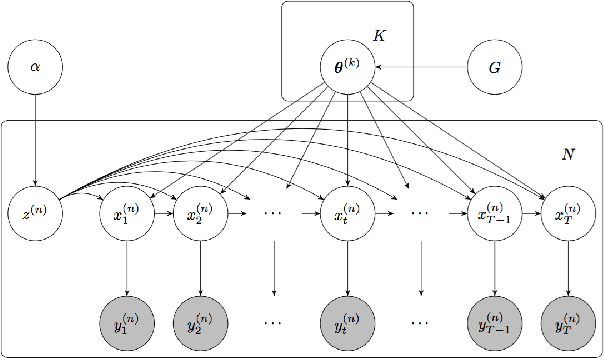
We propose a statistical framework for clustering multiple time series that exhibit nonlinear dynamics into an a-priori-unknown number of sub-groups that each comprise time series with similar dynamics. Our motivation comes from neuroscience where an important problem is to identify, within a large assembly of neurons, sub-groups that respond similarly to a stimulus or contingency. In the neural setting, conditioned on cluster membership and the parameters governing the dynamics, time series within a cluster are assumed independent and generated according to a nonlinear binomial state-space model. We derive a Metropolis-within-Gibbs algorithm for full Bayesian inference that alternates between sampling of cluster membership and sampling of parameters of interest. The Metropolis step is a PMMH iteration that requires an unbiased, low variance estimate of the likelihood function of a nonlinear state-space model. We leverage recent results on controlled sequential Monte Carlo to estimate likelihood functions more efficiently compared to the bootstrap particle filter. We apply the framework to time series acquired from the prefrontal cortex of mice in an experiment designed to characterize the neural underpinnings of fear.