Clustering Time Series with Nonlinear Dynamics: A Bayesian Non-Parametric and Particle-Based Approach
Paper and Code
Oct 24, 2018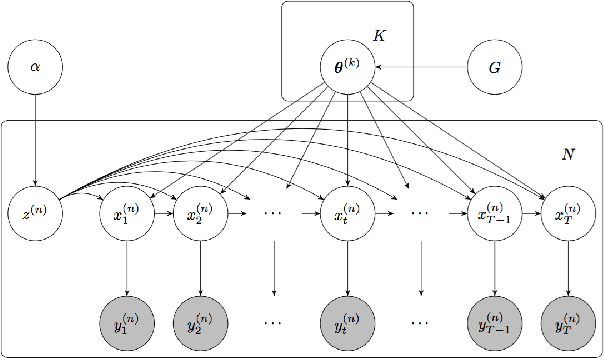



We propose a statistical framework for clustering multiple time series that exhibit nonlinear dynamics into an a-priori-unknown number of sub-groups that each comprise time series with similar dynamics. Our motivation comes from neuroscience where an important problem is to identify, within a large assembly of neurons, sub-groups that respond similarly to a stimulus or contingency. In the neural setting, conditioned on cluster membership and the parameters governing the dynamics, time series within a cluster are assumed independent and generated according to a nonlinear binomial state-space model. We derive a Metropolis-within-Gibbs algorithm for full Bayesian inference that alternates between sampling of cluster membership and sampling of parameters of interest. The Metropolis step is a PMMH iteration that requires an unbiased, low variance estimate of the likelihood function of a nonlinear state-space model. We leverage recent results on controlled sequential Monte Carlo to estimate likelihood functions more efficiently compared to the bootstrap particle filter. We apply the framework to time series acquired from the prefrontal cortex of mice in an experiment designed to characterize the neural underpinnings of fear.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge