Implementing Finite Impulse Response Filters on Quantum Computers

While signal processing is a mature area, its connections with quantum computing have received less attention. In this work, we propose approaches that perform classical discrete-time signal processing using quantum systems. Our approaches encode the classical discrete-time input signal into quantum states, and design unitaries to realize classical concepts of finite impulse response (FIR) filters. We also develop strategies to cascade lower-order filters to realize higher-order filters through designing appropriate unitary operators. Finally, a few directions for processing quantum states on classical systems after converting them to classical signals are suggested for future work.

Group Testing with Side Information via Generalized Approximate Message Passing

Group testing can help maintain a widespread testing program using fewer resources amid a pandemic. In a group testing setup, we are given n samples, one per individual. Each individual is either infected or uninfected. These samples are arranged into m < n pooled samples, where each pool is obtained by mixing a subset of the n individual samples. Infected individuals are then identified using a group testing algorithm. In this paper, we incorporate side information (SI) collected from contact tracing (CT) into nonadaptive/single-stage group testing algorithms. We generate different types of possible CT SI data by incorporating different possible characteristics of the spread of the disease. These data are fed into a group testing framework based on generalized approximate message passing (GAMP). Numerical results show that our GAMP-based algorithms provide improved accuracy. Compared to a loopy belief propagation algorithm, our proposed framework can increase the success probability by 0.25 for a group testing problem of n = 500 individuals with m = 100 pooled samples.

Mismatched Estimation in the Distance Geometry Problem

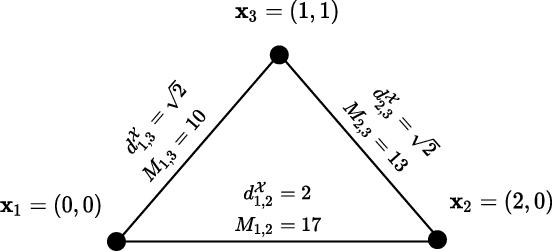
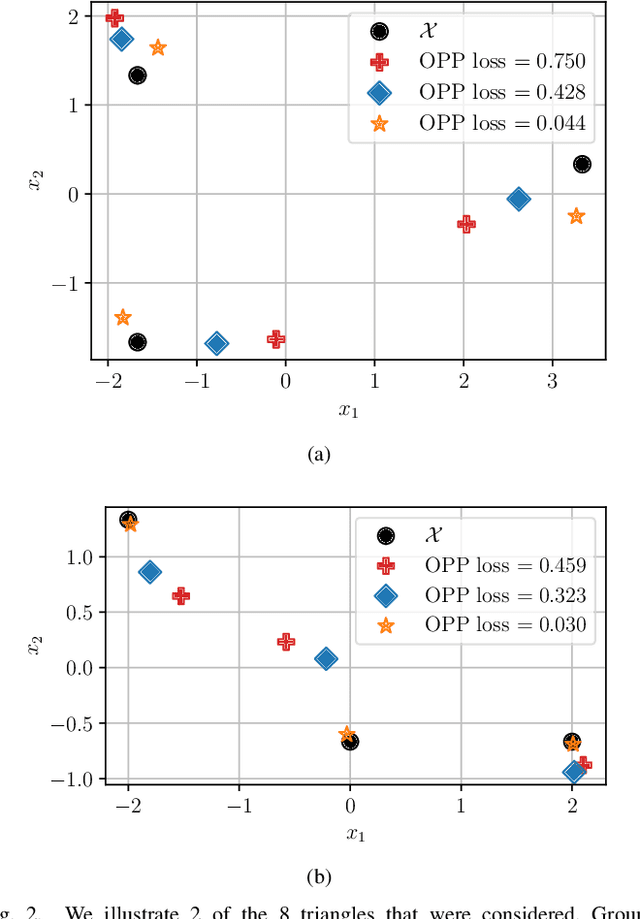
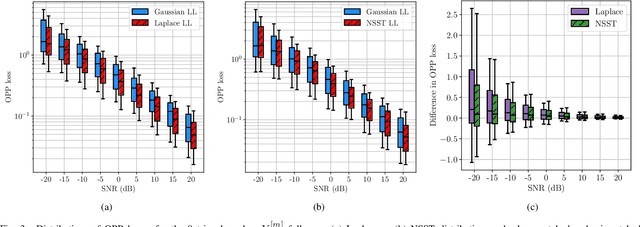
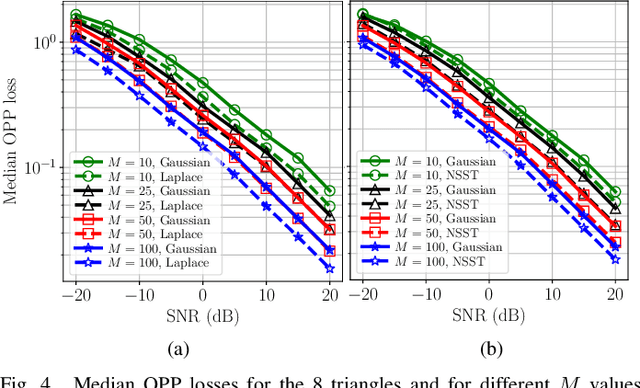
We investigate mismatched estimation in the context of the distance geometry problem (DGP). In the DGP, for a set of points, we are given noisy measurements of pairwise distances between the points, and our objective is to determine the geometric locations of the points. A common approach to deal with noisy measurements of pairwise distances is to compute least-squares estimates of the locations of the points. However, these least-squares estimates are likely to be suboptimal, because they do not necessarily maximize the correct likelihood function. In this paper, we argue that more accurate estimates can be obtained when an estimation procedure using the correct likelihood function of noisy measurements is performed. Our numerical results demonstrate that least-squares estimates can be suboptimal by several dB.

Gradient Obfuscation Gives a False Sense of Security in Federated Learning

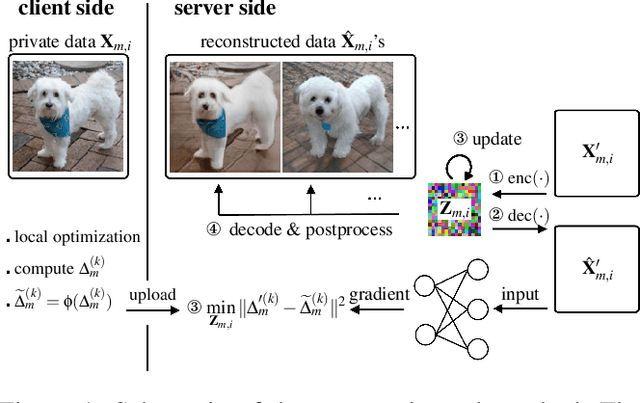
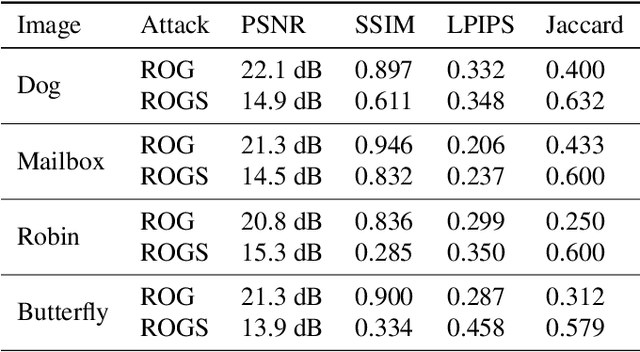
Federated learning has been proposed as a privacy-preserving machine learning framework that enables multiple clients to collaborate without sharing raw data. However, client privacy protection is not guaranteed by design in this framework. Prior work has shown that the gradient sharing strategies in federated learning can be vulnerable to data reconstruction attacks. In practice, though, clients may not transmit raw gradients considering the high communication cost or due to privacy enhancement requirements. Empirical studies have demonstrated that gradient obfuscation, including intentional obfuscation via gradient noise injection and unintentional obfuscation via gradient compression, can provide more privacy protection against reconstruction attacks. In this work, we present a new data reconstruction attack framework targeting the image classification task in federated learning. We show that commonly adopted gradient postprocessing procedures, such as gradient quantization, gradient sparsification, and gradient perturbation, may give a false sense of security in federated learning. Contrary to prior studies, we argue that privacy enhancement should not be treated as a byproduct of gradient compression. Additionally, we design a new method under the proposed framework to reconstruct the image at the semantic level. We quantify the semantic privacy leakage and compare with conventional based on image similarity scores. Our comparisons challenge the image data leakage evaluation schemes in the literature. The results emphasize the importance of revisiting and redesigning the privacy protection mechanisms for client data in existing federated learning algorithms.

Neural Tangent Kernel Empowered Federated Learning

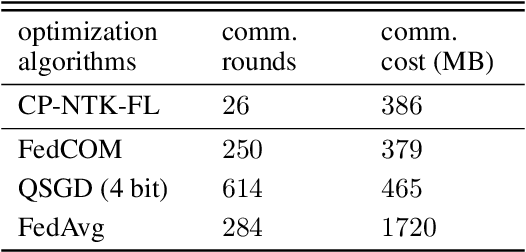
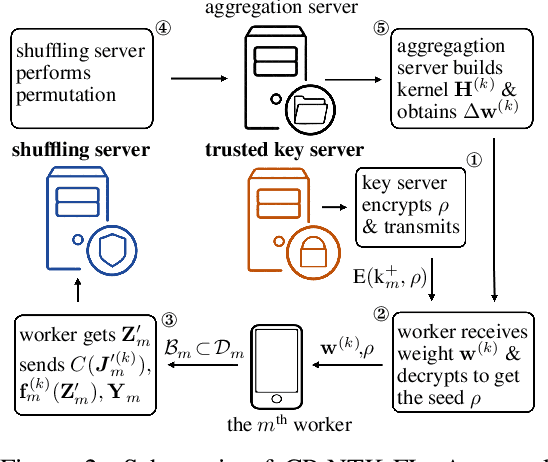
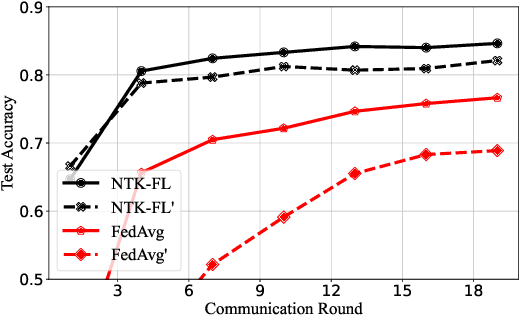
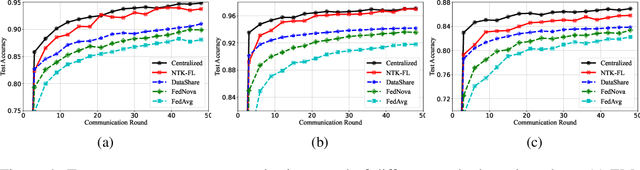
Federated learning (FL) is a privacy-preserving paradigm where multiple participants jointly solve a machine learning problem without sharing raw data. Unlike traditional distributed learning, a unique characteristic of FL is statistical heterogeneity, namely, data distributions across participants are different from each other. Meanwhile, recent advances in the interpretation of neural networks have seen a wide use of neural tangent kernel (NTK) for convergence and generalization analyses. In this paper, we propose a novel FL paradigm empowered by the NTK framework. The proposed paradigm addresses the challenge of statistical heterogeneity by transmitting update data that are more expressive than those of the traditional FL paradigms. Specifically, sample-wise Jacobian matrices, rather than model weights/gradients, are uploaded by participants. The server then constructs an empirical kernel matrix to update a global model without explicitly performing gradient descent. We further develop a variant with improved communication efficiency and enhanced privacy. Numerical results show that the proposed paradigm can achieve the same accuracy while reducing the number of communication rounds by an order of magnitude compared to federated averaging.

Noisy Pooled PCR for Virus Testing

Fast testing can help mitigate the coronavirus disease 2019 (COVID-19) pandemic. Despite their accuracy for single sample analysis, infectious diseases diagnostic tools, like RT-PCR, require substantial resources to test large populations. We develop a scalable approach for determining the viral status of pooled patient samples. Our approach converts group testing to a linear inverse problem, where false positives and negatives are interpreted as generated by a noisy communication channel, and a message passing algorithm estimates the illness status of patients. Numerical results reveal that our approach estimates patient illness using fewer pooled measurements than existing noisy group testing algorithms. Our approach can easily be extended to various applications, including where false negatives must be minimized. Finally, in a Utopian world we would have collaborated with RT-PCR experts; it is difficult to form such connections during a pandemic. We welcome new collaborators to reach out and help improve this work!

Rigorous State Evolution Analysis for Approximate Message Passing with Side Information

A common goal in many research areas is to reconstruct an unknown signal x from noisy linear measurements. Approximate message passing (AMP) is a class of low-complexity algorithms that can be used for efficiently solving such high-dimensional regression tasks. Often, it is the case that side information (SI) is available during reconstruction. For this reason, a novel algorithmic framework that incorporates SI into AMP, referred to as approximate message passing with side information (AMP-SI), has been recently introduced. In this work, we provide rigorous performance guarantees for AMP-SI when there are statistical dependencies between the signal and SI pairs and the entries of the measurement matrix are independent and identically distributed Gaussian. The AMP-SI performance is shown to be provably tracked by a scalar iteration referred to as state evolution. Moreover, we provide numerical examples that demonstrate empirically that the SE can predict the AMP-SI mean square error accurately.

Performance Trade-Offs in Multi-Processor Approximate Message Passing

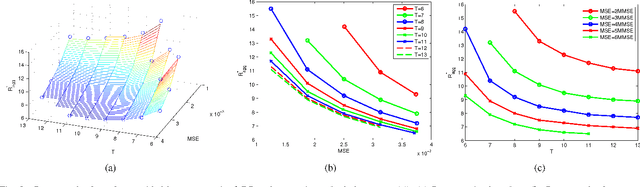
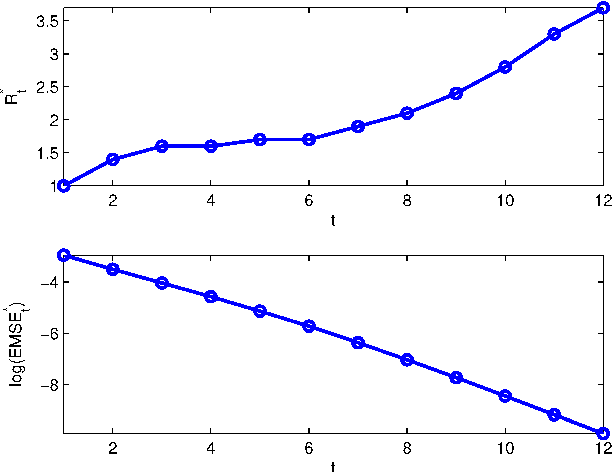
We consider large-scale linear inverse problems in Bayesian settings. Our general approach follows a recent line of work that applies the approximate message passing (AMP) framework in multi-processor (MP) computational systems by storing and processing a subset of rows of the measurement matrix along with corresponding measurements at each MP node. In each MP-AMP iteration, nodes of the MP system and its fusion center exchange lossily compressed messages pertaining to their estimates of the input. There is a trade-off between the physical costs of the reconstruction process including computation time, communication loads, and the reconstruction quality, and it is impossible to simultaneously minimize all the costs. We pose this minimization as a multi-objective optimization problem (MOP), and study the properties of the best trade-offs (Pareto optimality) in this MOP. We prove that the achievable region of this MOP is convex, and conjecture how the combined cost of computation and communication scales with the desired mean squared error. These properties are verified numerically.