Junan Zhu
Noisy Pooled PCR for Virus Testing
Apr 06, 2020


Abstract:Fast testing can help mitigate the coronavirus disease 2019 (COVID-19) pandemic. Despite their accuracy for single sample analysis, infectious diseases diagnostic tools, like RT-PCR, require substantial resources to test large populations. We develop a scalable approach for determining the viral status of pooled patient samples. Our approach converts group testing to a linear inverse problem, where false positives and negatives are interpreted as generated by a noisy communication channel, and a message passing algorithm estimates the illness status of patients. Numerical results reveal that our approach estimates patient illness using fewer pooled measurements than existing noisy group testing algorithms. Our approach can easily be extended to various applications, including where false negatives must be minimized. Finally, in a Utopian world we would have collaborated with RT-PCR experts; it is difficult to form such connections during a pandemic. We welcome new collaborators to reach out and help improve this work!
Performance Trade-Offs in Multi-Processor Approximate Message Passing
Apr 10, 2016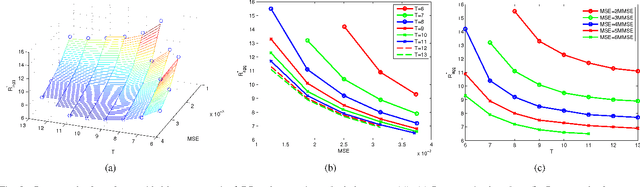
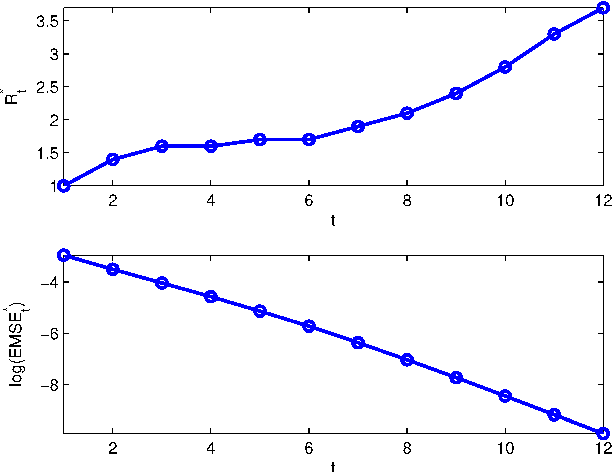
Abstract:We consider large-scale linear inverse problems in Bayesian settings. Our general approach follows a recent line of work that applies the approximate message passing (AMP) framework in multi-processor (MP) computational systems by storing and processing a subset of rows of the measurement matrix along with corresponding measurements at each MP node. In each MP-AMP iteration, nodes of the MP system and its fusion center exchange lossily compressed messages pertaining to their estimates of the input. There is a trade-off between the physical costs of the reconstruction process including computation time, communication loads, and the reconstruction quality, and it is impossible to simultaneously minimize all the costs. We pose this minimization as a multi-objective optimization problem (MOP), and study the properties of the best trade-offs (Pareto optimality) in this MOP. We prove that the achievable region of this MOP is convex, and conjecture how the combined cost of computation and communication scales with the desired mean squared error. These properties are verified numerically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge