Mahmoud Abdelkhalek
Mismatched Estimation in the Distance Geometry Problem
Jun 12, 2022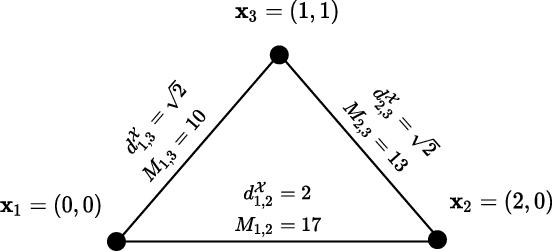
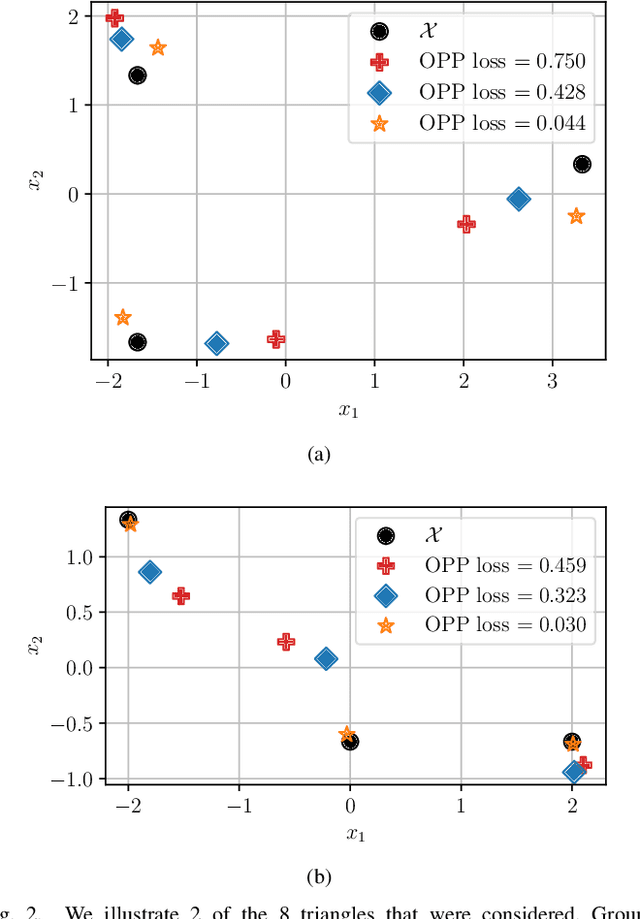
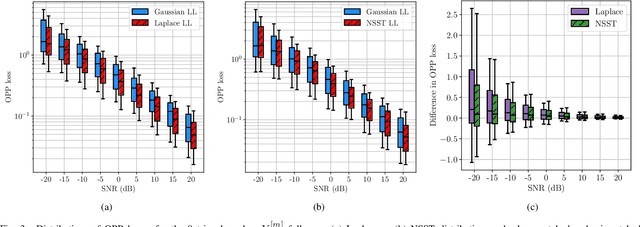
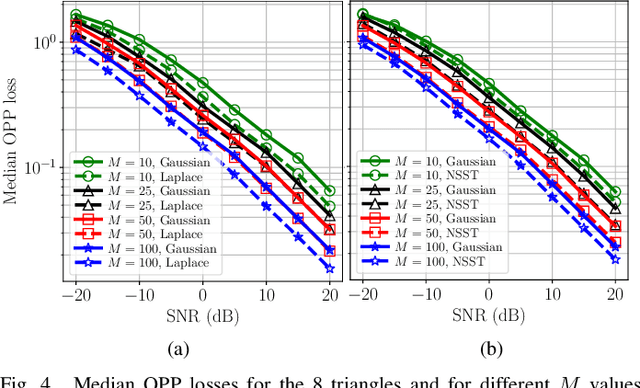
Abstract:We investigate mismatched estimation in the context of the distance geometry problem (DGP). In the DGP, for a set of points, we are given noisy measurements of pairwise distances between the points, and our objective is to determine the geometric locations of the points. A common approach to deal with noisy measurements of pairwise distances is to compute least-squares estimates of the locations of the points. However, these least-squares estimates are likely to be suboptimal, because they do not necessarily maximize the correct likelihood function. In this paper, we argue that more accurate estimates can be obtained when an estimation procedure using the correct likelihood function of noisy measurements is performed. Our numerical results demonstrate that least-squares estimates can be suboptimal by several dB.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge