Constrained Best Arm Identification in Grouped Bandits
Paper and Code
Dec 11, 2024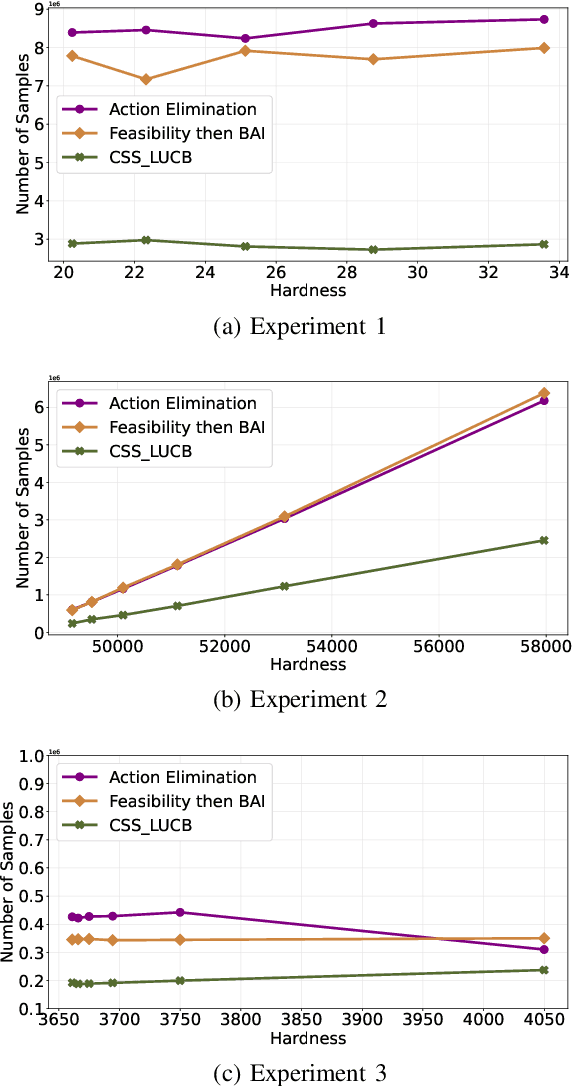
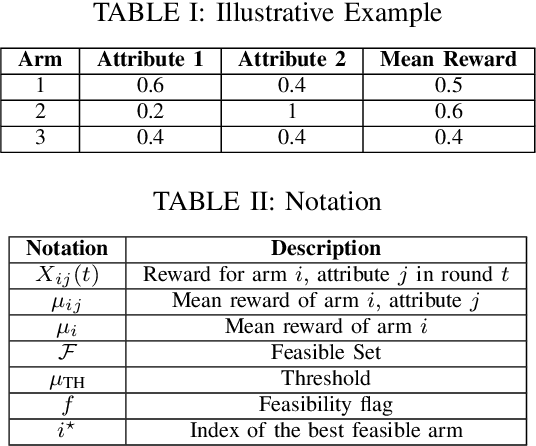
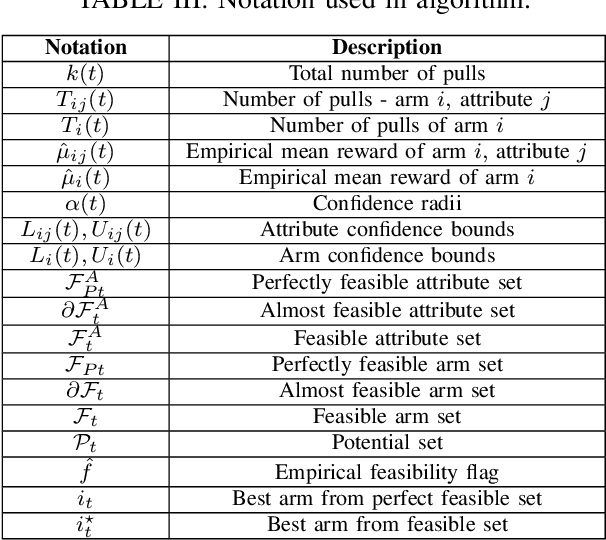
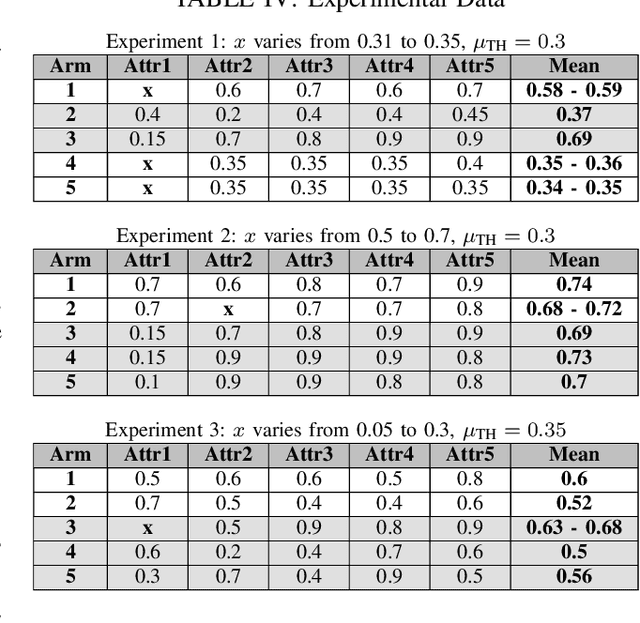
We study a grouped bandit setting where each arm comprises multiple independent sub-arms referred to as attributes. Each attribute of each arm has an independent stochastic reward. We impose the constraint that for an arm to be deemed feasible, the mean reward of all its attributes should exceed a specified threshold. The goal is to find the arm with the highest mean reward averaged across attributes among the set of feasible arms in the fixed confidence setting. We first characterize a fundamental limit on the performance of any policy. Following this, we propose a near-optimal confidence interval-based policy to solve this problem and provide analytical guarantees for the policy. We compare the performance of the proposed policy with that of two suitably modified versions of action elimination via simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge