Corrupted Multidimensional Binary Search: Learning in the Presence of Irrational Agents

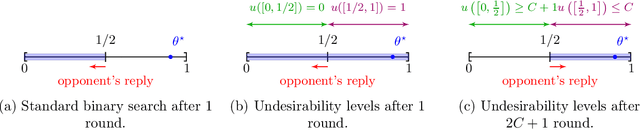
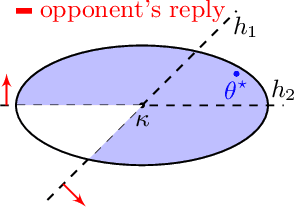
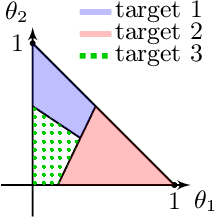
Standard game-theoretic formulations for settings like contextual pricing and security games assume that agents act in accordance with a specific behavioral model. In practice however, some agents may not prescribe to the dominant behavioral model or may act in ways that are arbitrarily inconsistent. Existing algorithms heavily depend on the model being (approximately) accurate for all agents and have poor performance in the presence of even a few such arbitrarily irrational agents. How do we design learning algorithms that are robust to the presence of arbitrarily irrational agents? We address this question for a number of canonical game-theoretic applications by designing a robust algorithm for the fundamental problem of multidimensional binary search. The performance of our algorithm degrades gracefully with the number of corrupted rounds, which correspond to irrational agents and need not be known in advance. As binary search is the key primitive in algorithms for contextual pricing, Stackelberg Security Games, and other game-theoretic applications, we immediately obtain robust algorithms for these settings. Our techniques draw inspiration from learning theory, game theory, high-dimensional geometry, and convex analysis, and may be of independent algorithmic interest.