Performance Control in Early Exiting to Deploy Large Models at the Same Cost of Smaller Ones

Early Exiting (EE) is a promising technique for speeding up inference by adaptively allocating compute resources to data points based on their difficulty. The approach enables predictions to exit at earlier layers for simpler samples while reserving more computation for challenging ones. In this study, we first present a novel perspective on the EE approach, showing that larger models deployed with EE can achieve higher performance than smaller models while maintaining similar computational costs. As existing EE approaches rely on confidence estimation at each exit point, we further study the impact of overconfidence on the controllability of the compute-performance trade-off. We introduce Performance Control Early Exiting (PCEE), a method that enables accuracy thresholding by basing decisions not on a data point's confidence but on the average accuracy of samples with similar confidence levels from a held-out validation set. In our experiments, we show that PCEE offers a simple yet computationally efficient approach that provides better control over performance than standard confidence-based approaches, and allows us to scale up model sizes to yield performance gain while reducing the computational cost.

Tight Lower Bounds and Improved Convergence in Performative Prediction

Performative prediction is a framework accounting for the shift in the data distribution induced by the prediction of a model deployed in the real world. Ensuring rapid convergence to a stable solution where the data distribution remains the same after the model deployment is crucial, especially in evolving environments. This paper extends the Repeated Risk Minimization (RRM) framework by utilizing historical datasets from previous retraining snapshots, yielding a class of algorithms that we call Affine Risk Minimizers and enabling convergence to a performatively stable point for a broader class of problems. We introduce a new upper bound for methods that use only the final iteration of the dataset and prove for the first time the tightness of both this new bound and the previous existing bounds within the same regime. We also prove that utilizing historical datasets can surpass the lower bound for last iterate RRM, and empirically observe faster convergence to the stable point on various performative prediction benchmarks. We offer at the same time the first lower bound analysis for RRM within the class of Affine Risk Minimizers, quantifying the potential improvements in convergence speed that could be achieved with other variants in our framework.

Performative Prediction on Games and Mechanism Design

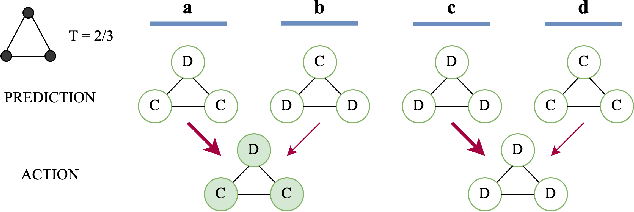
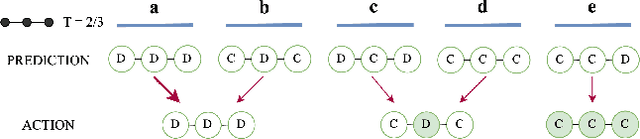
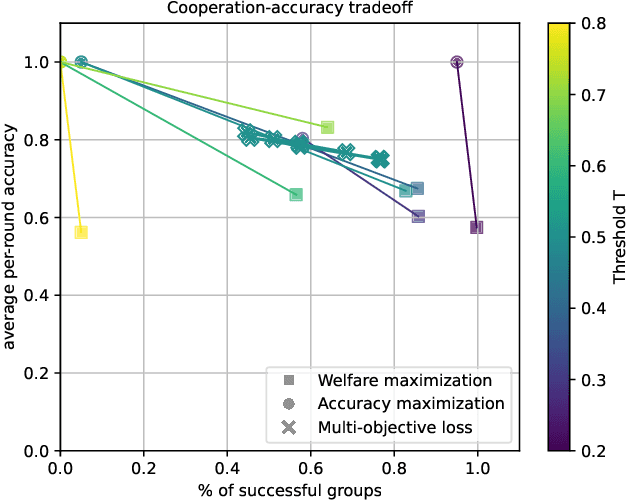
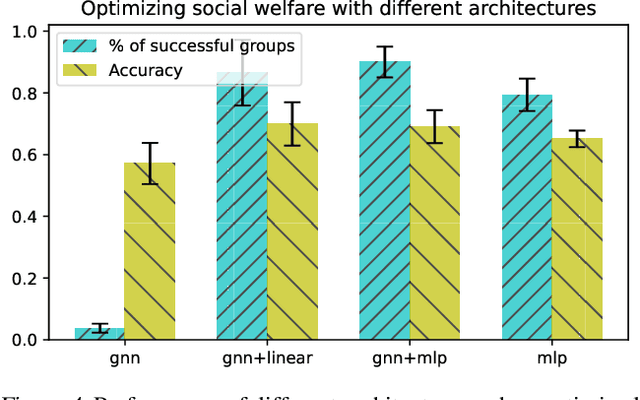
Predictions often influence the reality which they aim to predict, an effect known as performativity. Existing work focuses on accuracy maximization under this effect, but model deployment may have important unintended impacts, especially in multiagent scenarios. In this work, we investigate performative prediction in a concrete game-theoretic setting where social welfare is an alternative objective to accuracy maximization. We explore a collective risk dilemma scenario where maximising accuracy can negatively impact social welfare, when predicting collective behaviours. By assuming knowledge of a Bayesian agent behavior model, we then show how to achieve better trade-offs and use them for mechanism design.

Performative Prediction with Neural Networks

Performative prediction is a framework for learning models that influence the data they intend to predict. We focus on finding classifiers that are performatively stable, i.e. optimal for the data distribution they induce. Standard convergence results for finding a performatively stable classifier with the method of repeated risk minimization assume that the data distribution is Lipschitz continuous to the model's parameters. Under this assumption, the loss must be strongly convex and smooth in these parameters; otherwise, the method will diverge for some problems. In this work, we instead assume that the data distribution is Lipschitz continuous with respect to the model's predictions, a more natural assumption for performative systems. As a result, we are able to significantly relax the assumptions on the loss function. In particular, we do not need to assume convexity with respect to the model's parameters. As an illustration, we introduce a resampling procedure that models realistic distribution shifts and show that it satisfies our assumptions. We support our theory by showing that one can learn performatively stable classifiers with neural networks making predictions about real data that shift according to our proposed procedure.