Fangshuo Liao
Guided by the Experts: Provable Feature Learning Dynamic of Soft-Routed Mixture-of-Experts
Oct 08, 2025

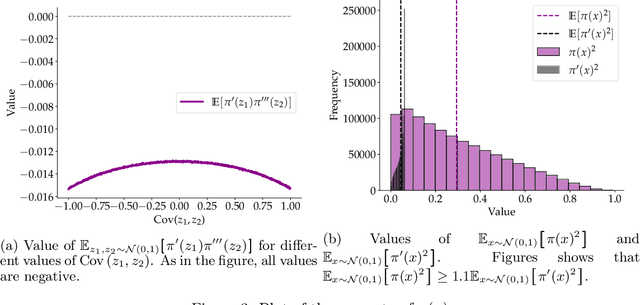
Abstract:Mixture-of-Experts (MoE) architectures have emerged as a cornerstone of modern AI systems. In particular, MoEs route inputs dynamically to specialized experts whose outputs are aggregated through weighted summation. Despite their widespread application, theoretical understanding of MoE training dynamics remains limited to either separate expert-router optimization or only top-1 routing scenarios with carefully constructed datasets. This paper advances MoE theory by providing convergence guarantees for joint training of soft-routed MoE models with non-linear routers and experts in a student-teacher framework. We prove that, with moderate over-parameterization, the student network undergoes a feature learning phase, where the router's learning process is ``guided'' by the experts, that recovers the teacher's parameters. Moreover, we show that a post-training pruning can effectively eliminate redundant neurons, followed by a provably convergent fine-tuning process that reaches global optimality. To our knowledge, our analysis is the first to bring novel insights in understanding the optimization landscape of the MoE architecture.
Provable Model-Parallel Distributed Principal Component Analysis with Parallel Deflation
Feb 24, 2025Abstract:We study a distributed Principal Component Analysis (PCA) framework where each worker targets a distinct eigenvector and refines its solution by updating from intermediate solutions provided by peers deemed as "superior". Drawing intuition from the deflation method in centralized eigenvalue problems, our approach breaks the sequential dependency in the deflation steps and allows asynchronous updates of workers, while incurring only a small communication cost. To our knowledge, a gap in the literature -- the theoretical underpinning of such distributed, dynamic interactions among workers -- has remained unaddressed. This paper offers a theoretical analysis explaining why, how, and when these intermediate, hierarchical updates lead to practical and provable convergence in distributed environments. Despite being a theoretical work, our prototype implementation demonstrates that such a distributed PCA algorithm converges effectively and in scalable way: through experiments, our proposed framework offers comparable performance to EigenGame-$\mu$, the state-of-the-art model-parallel PCA solver.
On the Error-Propagation of Inexact Deflation for Principal Component Analysis
Oct 06, 2023
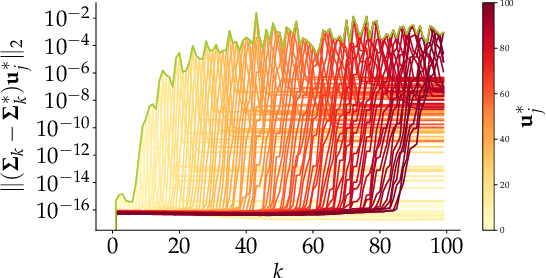
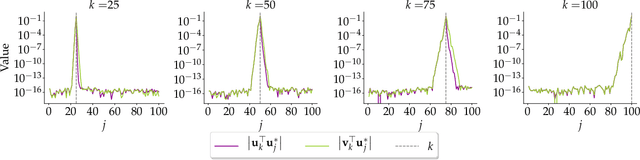
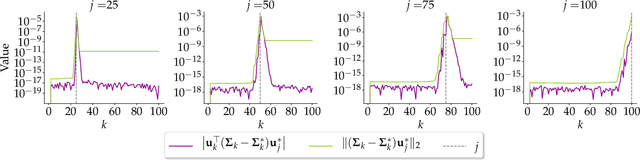
Abstract:Principal Component Analysis (PCA) is a popular tool in data analysis, especially when the data is high-dimensional. PCA aims to find subspaces, spanned by the so-called \textit{principal components}, that best explain the variance in the dataset. The deflation method is a popular meta-algorithm -- used to discover such subspaces -- that sequentially finds individual principal components, starting from the most important one and working its way towards the less important ones. However, due to its sequential nature, the numerical error introduced by not estimating principal components exactly -- e.g., due to numerical approximations through this process -- propagates, as deflation proceeds. To the best of our knowledge, this is the first work that mathematically characterizes the error propagation of the inexact deflation method, and this is the key contribution of this paper. We provide two main results: $i)$ when the sub-routine for finding the leading eigenvector is generic, and $ii)$ when power iteration is used as the sub-routine. In the latter case, the additional directional information from power iteration allows us to obtain a tighter error bound than the analysis of the sub-routine agnostic case. As an outcome, we provide explicit characterization on how the error progresses and affects subsequent principal component estimations for this fundamental problem.
Accelerated Convergence of Nesterov's Momentum for Deep Neural Networks under Partial Strong Convexity
Jun 13, 2023
Abstract:Current state-of-the-art analyses on the convergence of gradient descent for training neural networks focus on characterizing properties of the loss landscape, such as the Polyak-Lojaciewicz (PL) condition and the restricted strong convexity. While gradient descent converges linearly under such conditions, it remains an open question whether Nesterov's momentum enjoys accelerated convergence under similar settings and assumptions. In this work, we consider a new class of objective functions, where only a subset of the parameters satisfies strong convexity, and show Nesterov's momentum achieves acceleration in theory for this objective class. We provide two realizations of the problem class, one of which is deep ReLU networks, which --to the best of our knowledge--constitutes this work the first that proves accelerated convergence rate for non-trivial neural network architectures.
Scissorhands: Exploiting the Persistence of Importance Hypothesis for LLM KV Cache Compression at Test Time
May 26, 2023



Abstract:Large language models(LLMs) have sparked a new wave of exciting AI applications. Hosting these models at scale requires significant memory resources. One crucial memory bottleneck for the deployment stems from the context window. It is commonly recognized that model weights are memory hungry; however, the size of key-value embedding stored during the generation process (KV cache) can easily surpass the model size. The enormous size of the KV cache puts constraints on the inference batch size, which is crucial for high throughput inference workload. Inspired by an interesting observation of the attention scores, we hypothesize the persistence of importance: only pivotal tokens, which had a substantial influence at one step, will significantly influence future generations. Based on our empirical verification and theoretical analysis around this hypothesis, we propose Scissorhands, a system that maintains the memory usage of the KV cache at a fixed budget without finetuning the model. In essence, Scissorhands manages the KV cache by storing the pivotal tokens with a higher probability. We validate that Scissorhands reduces the inference memory usage of the KV cache by up to 5X without compromising model quality. We further demonstrate that Scissorhands can be combined with 4-bit quantization, traditionally used to compress model weights, to achieve up to 20X compression.
Strong Lottery Ticket Hypothesis with $\varepsilon$--perturbation
Oct 29, 2022



Abstract:The strong Lottery Ticket Hypothesis (LTH) claims the existence of a subnetwork in a sufficiently large, randomly initialized neural network that approximates some target neural network without the need of training. We extend the theoretical guarantee of the strong LTH literature to a scenario more similar to the original LTH, by generalizing the weight change in the pre-training step to some perturbation around initialization. In particular, we focus on the following open questions: By allowing an $\varepsilon$-scale perturbation on the random initial weights, can we reduce the over-parameterization requirement for the candidate network in the strong LTH? Furthermore, does the weight change by SGD coincide with a good set of such perturbation? We answer the first question by first extending the theoretical result on subset sum to allow perturbation on the candidates. Applying this result to the neural network setting, we show that such $\varepsilon$-perturbation reduces the over-parameterization requirement of the strong LTH. To answer the second question, we show via experiments that the perturbed weight achieved by the projected SGD shows better performance under the strong LTH pruning.
LOFT: Finding Lottery Tickets through Filter-wise Training
Oct 28, 2022
Abstract:Recent work on the Lottery Ticket Hypothesis (LTH) shows that there exist ``\textit{winning tickets}'' in large neural networks. These tickets represent ``sparse'' versions of the full model that can be trained independently to achieve comparable accuracy with respect to the full model. However, finding the winning tickets requires one to \emph{pretrain} the large model for at least a number of epochs, which can be a burdensome task, especially when the original neural network gets larger. In this paper, we explore how one can efficiently identify the emergence of such winning tickets, and use this observation to design efficient pretraining algorithms. For clarity of exposition, our focus is on convolutional neural networks (CNNs). To identify good filters, we propose a novel filter distance metric that well-represents the model convergence. As our theory dictates, our filter analysis behaves consistently with recent findings of neural network learning dynamics. Motivated by these observations, we present the \emph{LOttery ticket through Filter-wise Training} algorithm, dubbed as \textsc{LoFT}. \textsc{LoFT} is a model-parallel pretraining algorithm that partitions convolutional layers by filters to train them independently in a distributed setting, resulting in reduced memory and communication costs during pretraining. Experiments show that \textsc{LoFT} $i)$ preserves and finds good lottery tickets, while $ii)$ it achieves non-trivial computation and communication savings, and maintains comparable or even better accuracy than other pretraining methods.
On the Convergence of Shallow Neural Network Training with Randomly Masked Neurons
Dec 05, 2021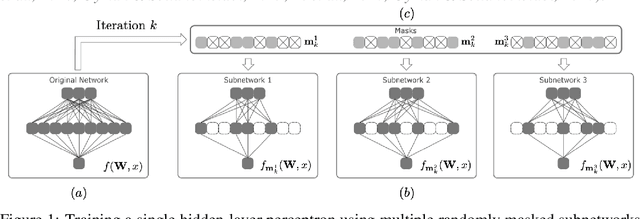
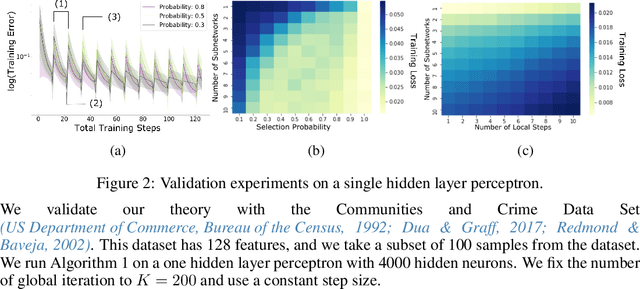
Abstract:Given a dense shallow neural network, we focus on iteratively creating, training, and combining randomly selected subnetworks (surrogate functions), towards training the full model. By carefully analyzing $i)$ the subnetworks' neural tangent kernel, $ii)$ the surrogate functions' gradient, and $iii)$ how we sample and combine the surrogate functions, we prove linear convergence rate of the training error -- within an error region -- for an overparameterized single-hidden layer perceptron with ReLU activations for a regression task. Our result implies that, for fixed neuron selection probability, the error term decreases as we increase the number of surrogate models, and increases as we increase the number of local training steps for each selected subnetwork. The considered framework generalizes and provides new insights on dropout training, multi-sample dropout training, as well as Independent Subnet Training; for each case, we provide corresponding convergence results, as corollaries of our main theorem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge