On the Convergence of Shallow Neural Network Training with Randomly Masked Neurons
Paper and Code
Dec 05, 2021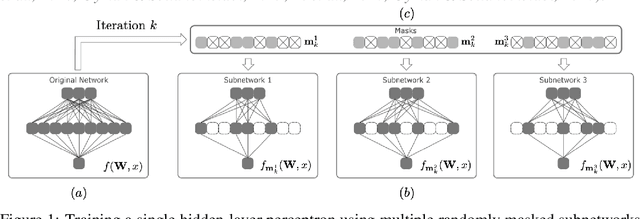
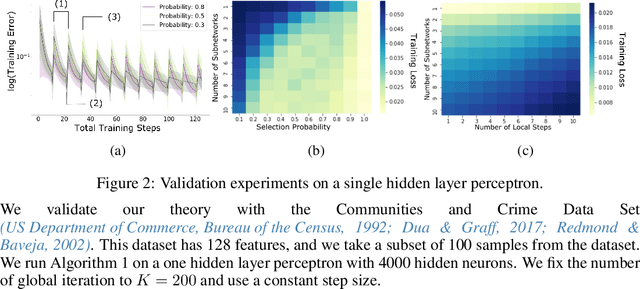
Given a dense shallow neural network, we focus on iteratively creating, training, and combining randomly selected subnetworks (surrogate functions), towards training the full model. By carefully analyzing $i)$ the subnetworks' neural tangent kernel, $ii)$ the surrogate functions' gradient, and $iii)$ how we sample and combine the surrogate functions, we prove linear convergence rate of the training error -- within an error region -- for an overparameterized single-hidden layer perceptron with ReLU activations for a regression task. Our result implies that, for fixed neuron selection probability, the error term decreases as we increase the number of surrogate models, and increases as we increase the number of local training steps for each selected subnetwork. The considered framework generalizes and provides new insights on dropout training, multi-sample dropout training, as well as Independent Subnet Training; for each case, we provide corresponding convergence results, as corollaries of our main theorem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge