The Role of Local Steps in Local SGD
Paper and Code
Mar 28, 2022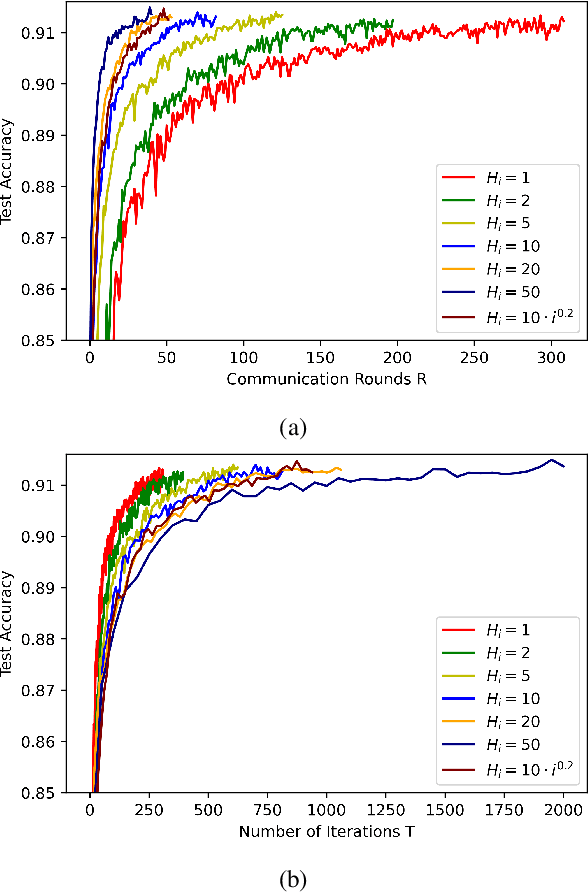
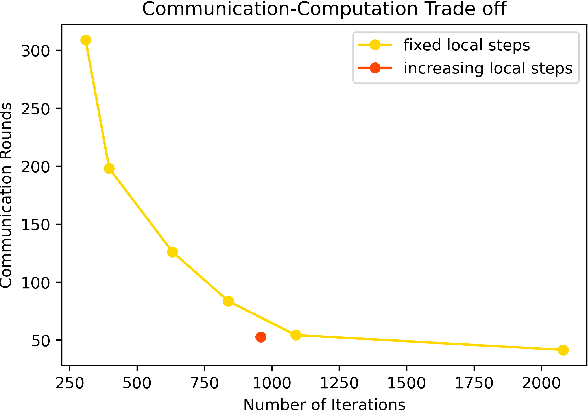
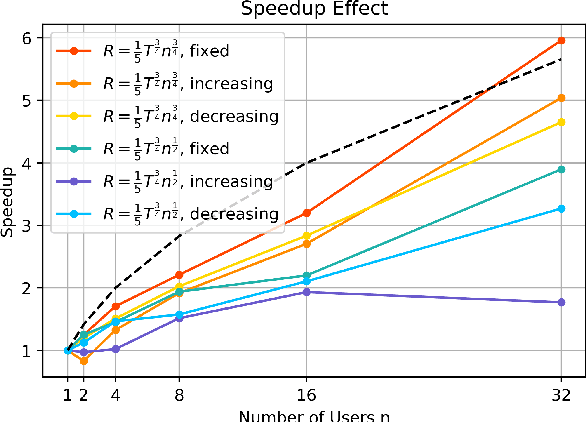
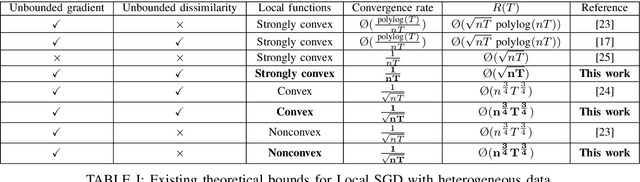
We consider the distributed stochastic optimization problem where $n$ agents want to minimize a global function given by the sum of agents' local functions, and focus on the heterogeneous setting when agents' local functions are defined over non-i.i.d. data sets. We study the Local SGD method, where agents perform a number of local stochastic gradient steps and occasionally communicate with a central node to improve their local optimization tasks. We analyze the effect of local steps on the convergence rate and the communication complexity of Local SGD. In particular, instead of assuming a fixed number of local steps across all communication rounds, we allow the number of local steps during the $i$-th communication round, $H_i$, to be different and arbitrary numbers. Our main contribution is to characterize the convergence rate of Local SGD as a function of $\{H_i\}_{i=1}^R$ under various settings of strongly convex, convex, and nonconvex local functions, where $R$ is the total number of communication rounds. Based on this characterization, we provide sufficient conditions on the sequence $\{H_i\}_{i=1}^R$ such that Local SGD can achieve linear speed-up with respect to the number of workers. Furthermore, we propose a new communication strategy with increasing local steps superior to existing communication strategies for strongly convex local functions. On the other hand, for convex and nonconvex local functions, we argue that fixed local steps are the best communication strategy for Local SGD and recover state-of-the-art convergence rate results. Finally, we justify our theoretical results through extensive numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge