Tiancheng Qin
Scalable and Independent Learning of Nash Equilibrium Policies in $n$-Player Stochastic Games with Unknown Independent Chains
Dec 04, 2023Abstract:We study a subclass of $n$-player stochastic games, namely, stochastic games with independent chains and unknown transition matrices. In this class of games, players control their own internal Markov chains whose transitions do not depend on the states/actions of other players. However, players' decisions are coupled through their payoff functions. We assume players can receive only realizations of their payoffs, and that the players can not observe the states and actions of other players, nor do they know the transition probability matrices of their own Markov chain. Relying on a compact dual formulation of the game based on occupancy measures and the technique of confidence set to maintain high-probability estimates of the unknown transition matrices, we propose a fully decentralized mirror descent algorithm to learn an $\epsilon$-NE for this class of games. The proposed algorithm has the desired properties of independence, scalability, and convergence. Specifically, under no assumptions on the reward functions, we show the proposed algorithm converges in polynomial time in a weaker distance (namely, the averaged Nikaido-Isoda gap) to the set of $\epsilon$-NE policies with arbitrarily high probability. Moreover, assuming the existence of a variationally stable Nash equilibrium policy, we show that the proposed algorithm converges asymptotically to the stable $\epsilon$-NE policy with arbitrarily high probability. In addition to Markov potential games and linear-quadratic stochastic games, this work provides another subclass of $n$-player stochastic games that, under some mild assumptions, admit polynomial-time learning algorithms for finding their stationary $\epsilon$-NE policies.
Local Environment Poisoning Attacks on Federated Reinforcement Learning
Mar 18, 2023



Abstract:Federated learning (FL) has become a popular tool for solving traditional Reinforcement Learning (RL) tasks. The multi-agent structure addresses the major concern of data-hungry in traditional RL, while the federated mechanism protects the data privacy of individual agents. However, the federated mechanism also exposes the system to poisoning by malicious agents that can mislead the trained policy. Despite the advantage brought by FL, the vulnerability of Federated Reinforcement Learning (FRL) has not been well-studied before. In this work, we propose the first general framework to characterize FRL poisoning as an optimization problem constrained by a limited budget and design a poisoning protocol that can be applied to policy-based FRL and extended to FRL with actor-critic as a local RL algorithm by training a pair of private and public critics. We also discuss a conventional defense strategy inherited from FL to mitigate this risk. We verify our poisoning effectiveness by conducting extensive experiments targeting mainstream RL algorithms and over various RL OpenAI Gym environments covering a wide range of difficulty levels. Our results show that our proposed defense protocol is successful in most cases but is not robust under complicated environments. Our work provides new insights into the vulnerability of FL in RL training and poses additional challenges for designing robust FRL algorithms.
Theta-Resonance: A Single-Step Reinforcement Learning Method for Design Space Exploration
Nov 17, 2022Abstract:Given an environment (e.g., a simulator) for evaluating samples in a specified design space and a set of weighted evaluation metrics -- one can use Theta-Resonance, a single-step Markov Decision Process (MDP), to train an intelligent agent producing progressively more optimal samples. In Theta-Resonance, a neural network consumes a constant input tensor and produces a policy as a set of conditional probability density functions (PDFs) for sampling each design dimension. We specialize existing policy gradient algorithms in deep reinforcement learning (D-RL) in order to use evaluation feedback (in terms of cost, penalty or reward) to update our policy network with robust algorithmic stability and minimal design evaluations. We study multiple neural architectures (for our policy network) within the context of a simple SoC design space and propose a method of constructing synthetic space exploration problems to compare and improve design space exploration (DSE) algorithms. Although we only present categorical design spaces, we also outline how to use Theta-Resonance in order to explore continuous and mixed continuous-discrete design spaces.
The Role of Local Steps in Local SGD
Mar 28, 2022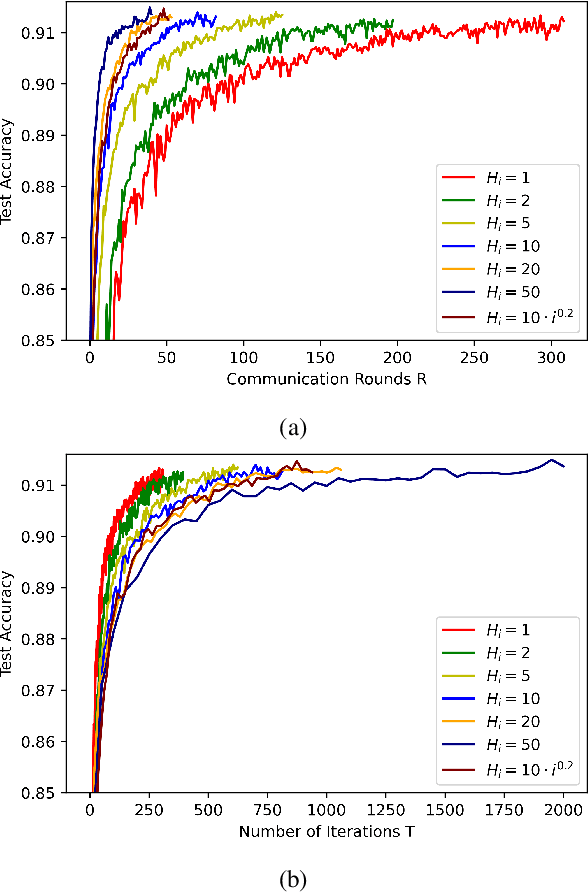
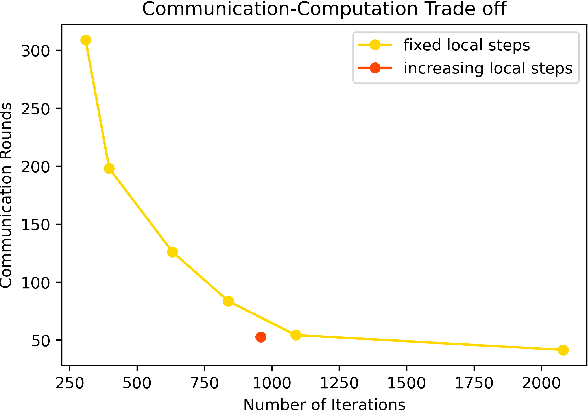
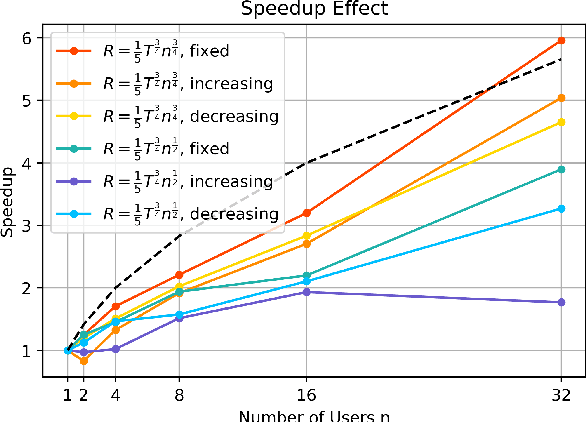
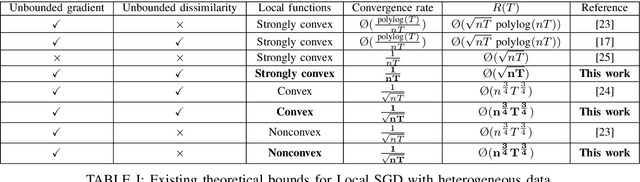
Abstract:We consider the distributed stochastic optimization problem where $n$ agents want to minimize a global function given by the sum of agents' local functions, and focus on the heterogeneous setting when agents' local functions are defined over non-i.i.d. data sets. We study the Local SGD method, where agents perform a number of local stochastic gradient steps and occasionally communicate with a central node to improve their local optimization tasks. We analyze the effect of local steps on the convergence rate and the communication complexity of Local SGD. In particular, instead of assuming a fixed number of local steps across all communication rounds, we allow the number of local steps during the $i$-th communication round, $H_i$, to be different and arbitrary numbers. Our main contribution is to characterize the convergence rate of Local SGD as a function of $\{H_i\}_{i=1}^R$ under various settings of strongly convex, convex, and nonconvex local functions, where $R$ is the total number of communication rounds. Based on this characterization, we provide sufficient conditions on the sequence $\{H_i\}_{i=1}^R$ such that Local SGD can achieve linear speed-up with respect to the number of workers. Furthermore, we propose a new communication strategy with increasing local steps superior to existing communication strategies for strongly convex local functions. On the other hand, for convex and nonconvex local functions, we argue that fixed local steps are the best communication strategy for Local SGD and recover state-of-the-art convergence rate results. Finally, we justify our theoretical results through extensive numerical experiments.
Faster Convergence of Local SGD for Over-Parameterized Models
Jan 30, 2022Abstract:Modern machine learning architectures are often highly expressive. They are usually over-parameterized and can interpolate the data by driving the empirical loss close to zero. We analyze the convergence of Local SGD (or FedAvg) for such over-parameterized models in the heterogeneous data setting and improve upon the existing literature by establishing the following convergence rates. We show an error bound of $\O(\exp(-T))$ for strongly-convex loss functions, where $T$ is the total number of iterations. For general convex loss functions, we establish an error bound of $\O(1/T)$ under a mild data similarity assumption and an error bound of $\O(K/T)$ otherwise, where $K$ is the number of local steps. We also extend our results for non-convex loss functions by proving an error bound of $\O(K/T)$. Before our work, the best-known convergence rate for strongly-convex loss functions was $\O(\exp(-T/K))$, and none existed for general convex or non-convex loss functions under the overparameterized setting. We complete our results by providing problem instances in which such convergence rates are tight to a constant factor under a reasonably small stepsize scheme. Finally, we validate our theoretical results using numerical experiments on real and synthetic data.
Communication-efficient Decentralized Local SGD over Undirected Networks
Nov 06, 2020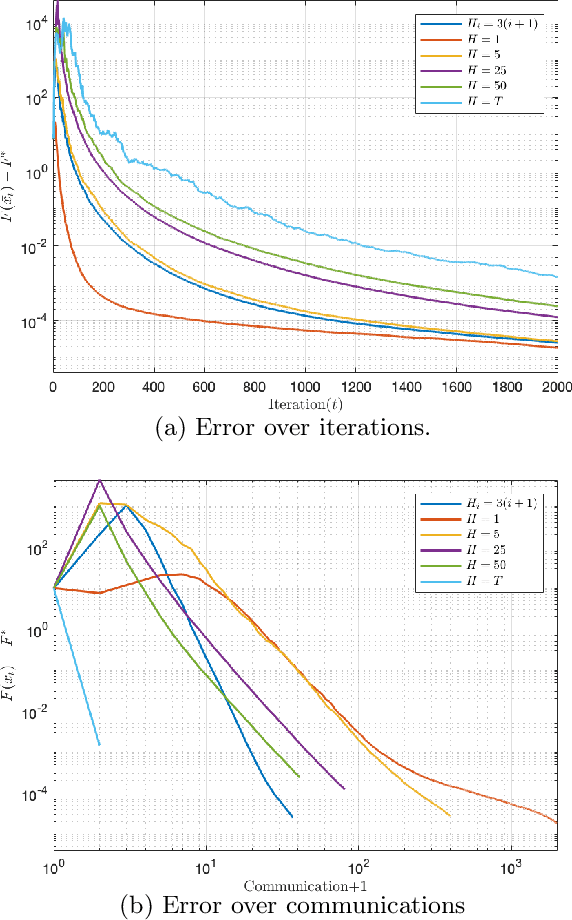
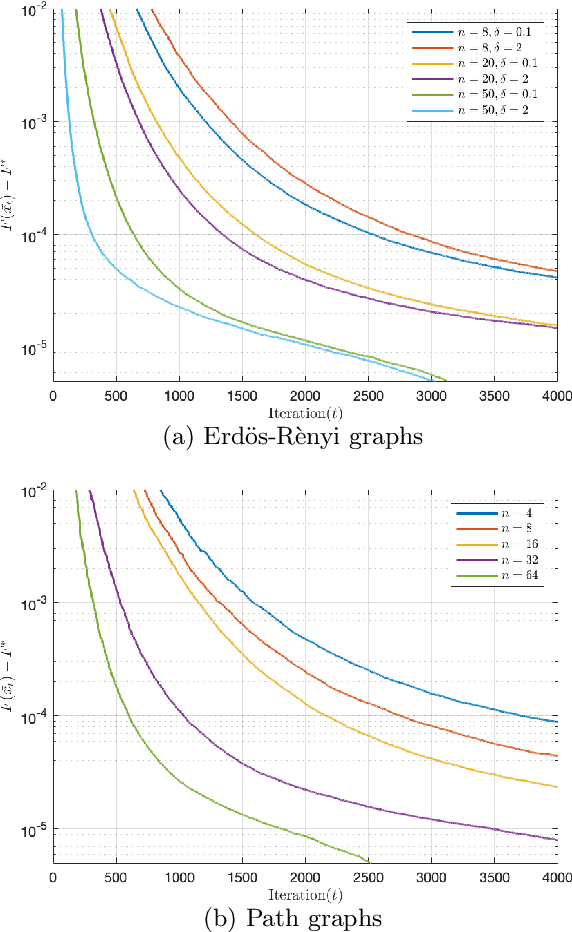
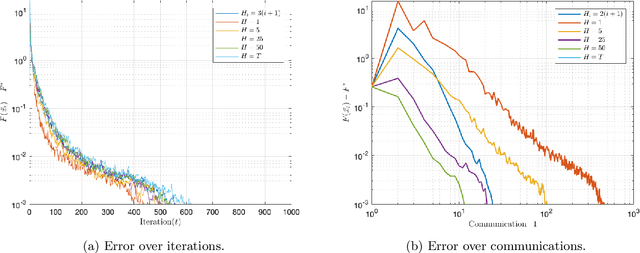
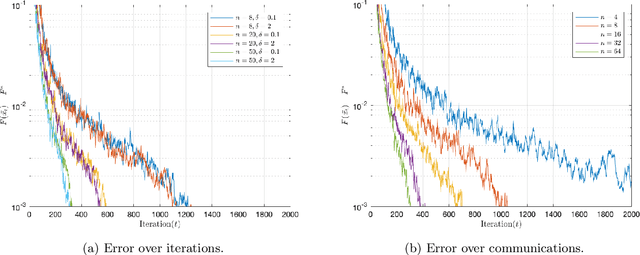
Abstract:We consider the distributed learning problem where a network of $n$ agents seeks to minimize a global function $F$. Agents have access to $F$ through noisy gradients, and they can locally communicate with their neighbors a network. We study the Decentralized Local SDG method, where agents perform a number of local gradient steps and occasionally exchange information with their neighbors. Previous algorithmic analysis efforts have focused on the specific network topology (star topology) where a leader node aggregates all agents' information. We generalize that setting to an arbitrary network by analyzing the trade-off between the number of communication rounds and the computational effort of each agent. We bound the expected optimality gap in terms of the number of iterates $T$, the number of workers $n$, and the spectral gap of the underlying network. Our main results show that by using only $R=\Omega(n)$ communication rounds, one can achieve an error that scales as $O({1}/{nT})$, where the number of communication rounds is independent of $T$ and only depends on the number of agents. Finally, we provide numerical evidence of our theoretical results through experiments on real and synthetic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge