A Theoretical Analysis of Soft-Label vs Hard-Label Training in Neural Networks

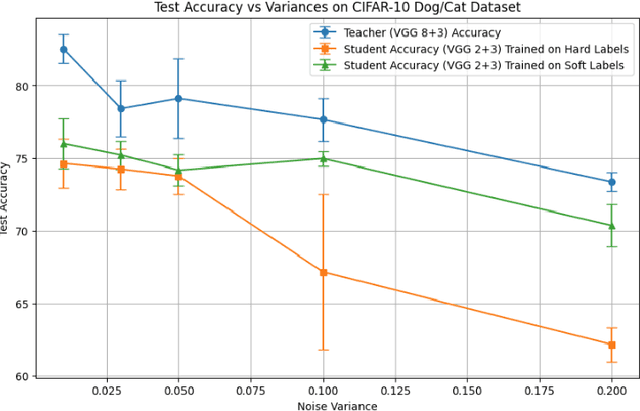
Knowledge distillation, where a small student model learns from a pre-trained large teacher model, has achieved substantial empirical success since the seminal work of \citep{hinton2015distilling}. Despite prior theoretical studies exploring the benefits of knowledge distillation, an important question remains unanswered: why does soft-label training from the teacher require significantly fewer neurons than directly training a small neural network with hard labels? To address this, we first present motivating experimental results using simple neural network models on a binary classification problem. These results demonstrate that soft-label training consistently outperforms hard-label training in accuracy, with the performance gap becoming more pronounced as the dataset becomes increasingly difficult to classify. We then substantiate these observations with a theoretical contribution based on two-layer neural network models. Specifically, we show that soft-label training using gradient descent requires only $O\left(\frac{1}{\gamma^2 \epsilon}\right)$ neurons to achieve a classification loss averaged over epochs smaller than some $\epsilon > 0$, where $\gamma$ is the separation margin of the limiting kernel. In contrast, hard-label training requires $O\left(\frac{1}{\gamma^4} \cdot \ln\left(\frac{1}{\epsilon}\right)\right)$ neurons, as derived from an adapted version of the gradient descent analysis in \citep{ji2020polylogarithmic}. This implies that when $\gamma \leq \epsilon$, i.e., when the dataset is challenging to classify, the neuron requirement for soft-label training can be significantly lower than that for hard-label training. Finally, we present experimental results on deep neural networks, further validating these theoretical findings.

A Comprehensive Survey of 3D Dense Captioning: Localizing and Describing Objects in 3D Scenes

Three-Dimensional (3D) dense captioning is an emerging vision-language bridging task that aims to generate multiple detailed and accurate descriptions for 3D scenes. It presents significant potential and challenges due to its closer representation of the real world compared to 2D visual captioning, as well as complexities in data collection and processing of 3D point cloud sources. Despite the popularity and success of existing methods, there is a lack of comprehensive surveys summarizing the advancements in this field, which hinders its progress. In this paper, we provide a comprehensive review of 3D dense captioning, covering task definition, architecture classification, dataset analysis, evaluation metrics, and in-depth prosperity discussions. Based on a synthesis of previous literature, we refine a standard pipeline that serves as a common paradigm for existing methods. We also introduce a clear taxonomy of existing models, summarize technologies involved in different modules, and conduct detailed experiment analysis. Instead of a chronological order introduction, we categorize the methods into different classes to facilitate exploration and analysis of the differences and connections among existing techniques. We also provide a reading guideline to assist readers with different backgrounds and purposes in reading efficiently. Furthermore, we propose a series of promising future directions for 3D dense captioning by identifying challenges and aligning them with the development of related tasks, offering valuable insights and inspiring future research in this field. Our aim is to provide a comprehensive understanding of 3D dense captioning, foster further investigations, and contribute to the development of novel applications in multimedia and related domains.

SPriFed-OMP: A Differentially Private Federated Learning Algorithm for Sparse Basis Recovery

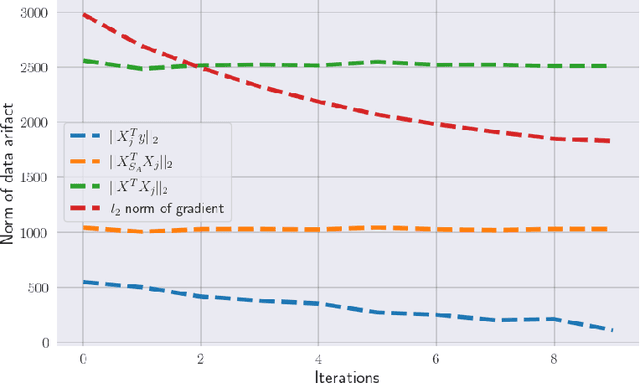
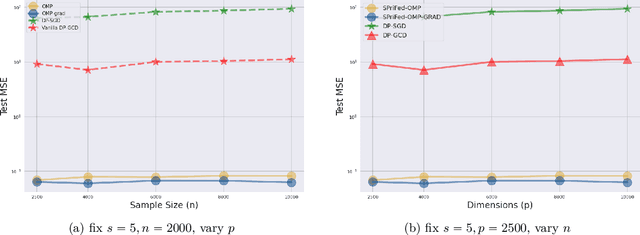
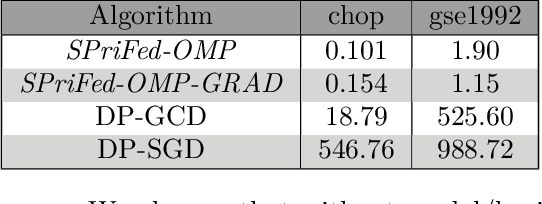
Sparse basis recovery is a classical and important statistical learning problem when the number of model dimensions $p$ is much larger than the number of samples $n$. However, there has been little work that studies sparse basis recovery in the Federated Learning (FL) setting, where the client data's differential privacy (DP) must also be simultaneously protected. In particular, the performance guarantees of existing DP-FL algorithms (such as DP-SGD) will degrade significantly when $p \gg n$, and thus, they will fail to learn the true underlying sparse model accurately. In this work, we develop a new differentially private sparse basis recovery algorithm for the FL setting, called SPriFed-OMP. SPriFed-OMP converts OMP (Orthogonal Matching Pursuit) to the FL setting. Further, it combines SMPC (secure multi-party computation) and DP to ensure that only a small amount of noise needs to be added in order to achieve differential privacy. As a result, SPriFed-OMP can efficiently recover the true sparse basis for a linear model with only $n = O(\sqrt{p})$ samples. We further present an enhanced version of our approach, SPriFed-OMP-GRAD based on gradient privatization, that improves the performance of SPriFed-OMP. Our theoretical analysis and empirical results demonstrate that both SPriFed-OMP and SPriFed-OMP-GRAD terminate in a small number of steps, and they significantly outperform the previous state-of-the-art DP-FL solutions in terms of the accuracy-privacy trade-off.

Top in Chinese Data Processing: English Code Models

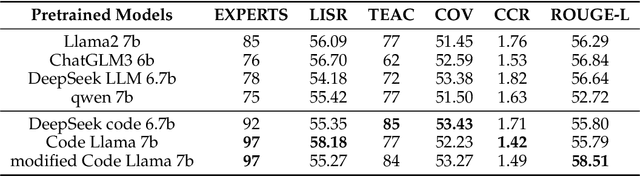
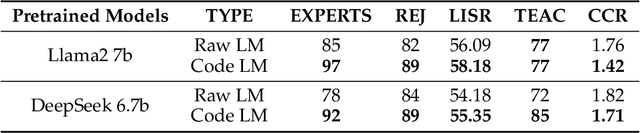
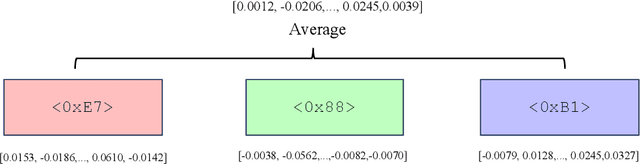
While the alignment between tasks and training corpora is a fundamental consensus in the application of language models, our series of experiments and the metrics we designed reveal that code-based Large Language Models (LLMs) significantly outperform models trained on data that is closely matched to the tasks in non-coding Chinese tasks. Moreover, in tasks high sensitivity to Chinese hallucinations, models exhibiting fewer linguistic features of the Chinese language achieve better performance. Our experimental results can be easily replicated in Chinese data processing tasks, such as preparing data for Retrieval-Augmented Generation (RAG), by simply replacing the base model with a code-based model. Additionally, our research offers a distinct perspective for discussion on the philosophical "Chinese Room" thought experiment.

On the Generalization Power of the Overfitted Three-Layer Neural Tangent Kernel Model

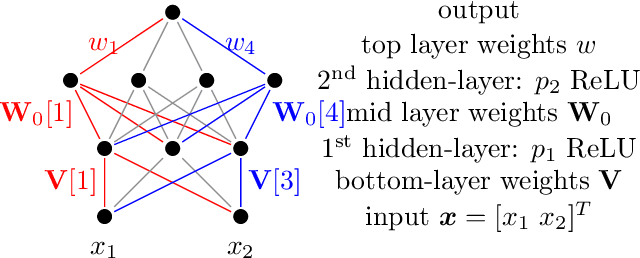
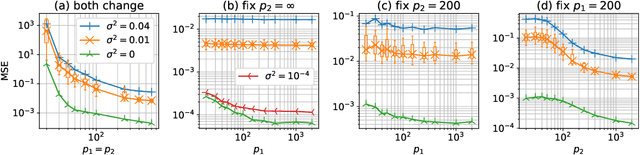
In this paper, we study the generalization performance of overparameterized 3-layer NTK models. We show that, for a specific set of ground-truth functions (which we refer to as the "learnable set"), the test error of the overfitted 3-layer NTK is upper bounded by an expression that decreases with the number of neurons of the two hidden layers. Different from 2-layer NTK where there exists only one hidden-layer, the 3-layer NTK involves interactions between two hidden-layers. Our upper bound reveals that, between the two hidden-layers, the test error descends faster with respect to the number of neurons in the second hidden-layer (the one closer to the output) than with respect to that in the first hidden-layer (the one closer to the input). We also show that the learnable set of 3-layer NTK without bias is no smaller than that of 2-layer NTK models with various choices of bias in the neurons. However, in terms of the actual generalization performance, our results suggest that 3-layer NTK is much less sensitive to the choices of bias than 2-layer NTK, especially when the input dimension is large.

SeedGNN: Graph Neural Networks for Supervised Seeded Graph Matching

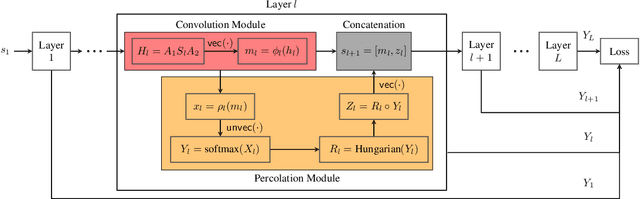
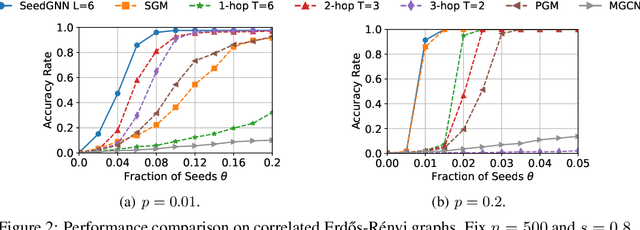
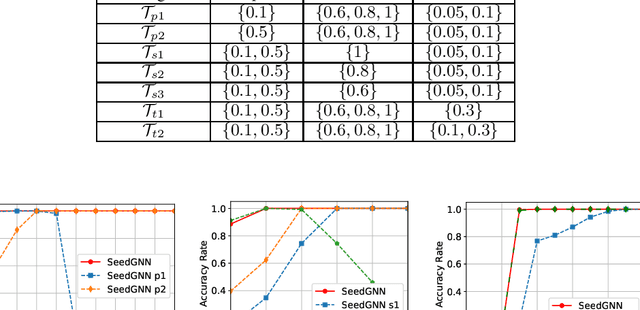
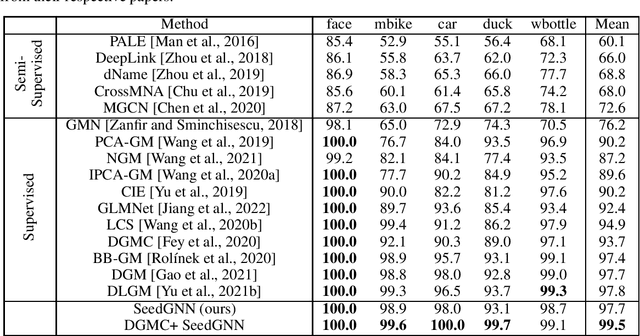
Recently, there have been significant interests in designing Graph Neural Networks (GNNs) for seeded graph matching, which aims to match two (unlabeled) graphs using only topological information and a small set of seeds. However, most previous GNN architectures for seeded graph matching employ a semi-supervised approach, which learns from only the seed set in a single pair of graphs, and therefore does not attempt to learn from many training examples/graphs to best match future unseen graphs. In contrast, this paper is the first to propose a supervised approach for seeded graph matching, which had so far only been used for seedless graph matching. Our proposed SeedGNN architecture employs a number of novel design choices that are inspired by theoretical studies of seeded graph matching. First, SeedGNN can easily learn the capability of counting and using witnesses of different hops, in a way that can be generalized to graphs with different sizes. Second, SeedGNN can use easily-matched pairs as new seeds to percolate and match other nodes. We evaluate SeedGNN on both synthetic and real graphs, and demonstrate significant performance improvement over both non-learning and learning algorithms in the existing literature. Further, our experiments confirm that the knowledge learned by SeedGNN from training graphs can be generalized to test graphs with different sizes and categories.

Student-Teacher Learning from Clean Inputs to Noisy Inputs

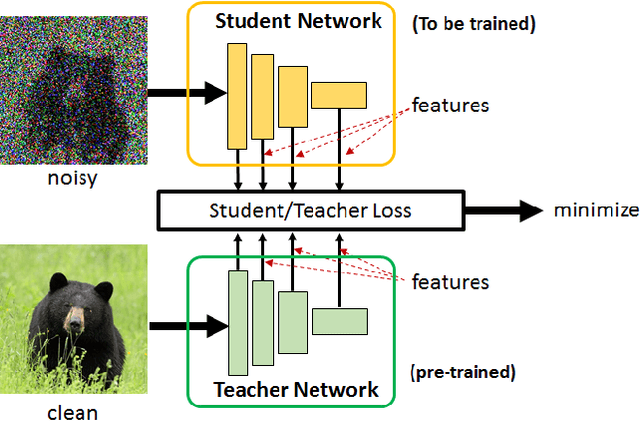
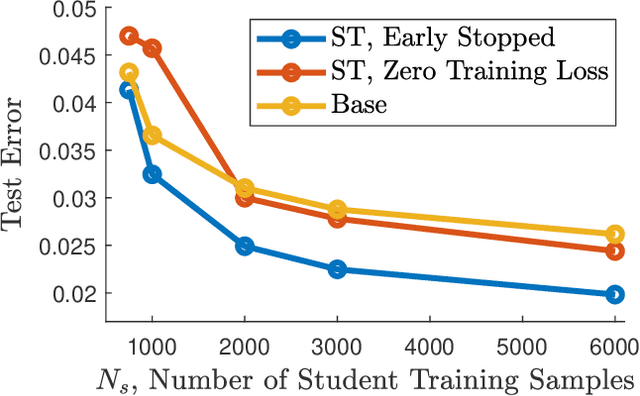
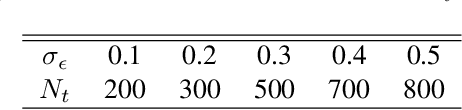
Feature-based student-teacher learning, a training method that encourages the student's hidden features to mimic those of the teacher network, is empirically successful in transferring the knowledge from a pre-trained teacher network to the student network. Furthermore, recent empirical results demonstrate that, the teacher's features can boost the student network's generalization even when the student's input sample is corrupted by noise. However, there is a lack of theoretical insights into why and when this method of transferring knowledge can be successful between such heterogeneous tasks. We analyze this method theoretically using deep linear networks, and experimentally using nonlinear networks. We identify three vital factors to the success of the method: (1) whether the student is trained to zero training loss; (2) how knowledgeable the teacher is on the clean-input problem; (3) how the teacher decomposes its knowledge in its hidden features. Lack of proper control in any of the three factors leads to failure of the student-teacher learning method.

On the Generalization Power of Overfitted Two-Layer Neural Tangent Kernel Models

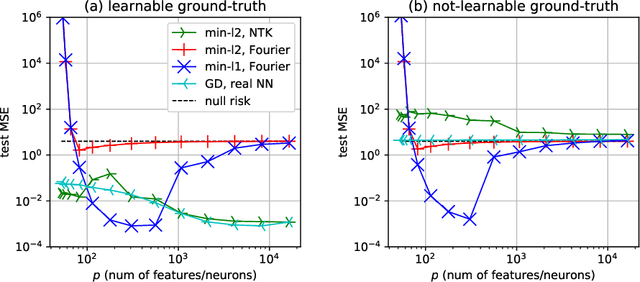
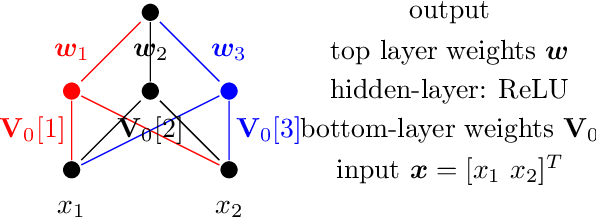
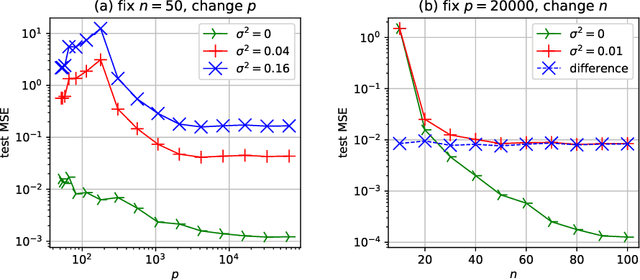
In this paper, we study the generalization performance of min $\ell_2$-norm overfitting solutions for the neural tangent kernel (NTK) model of a two-layer neural network. We show that, depending on the ground-truth function, the test error of overfitted NTK models exhibits characteristics that are different from the "double-descent" of other overparameterized linear models with simple Fourier or Gaussian features. Specifically, for a class of learnable functions, we provide a new upper bound of the generalization error that approaches a small limiting value, even when the number of neurons $p$ approaches infinity. This limiting value further decreases with the number of training samples $n$. For functions outside of this class, we provide a lower bound on the generalization error that does not diminish to zero even when $n$ and $p$ are both large.

The Power of $D$-hops in Matching Power-Law Graphs

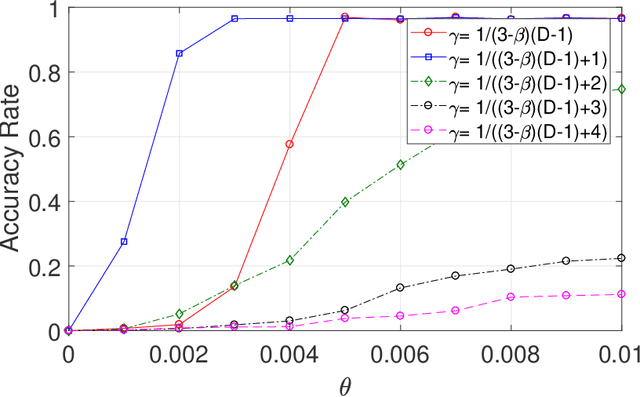
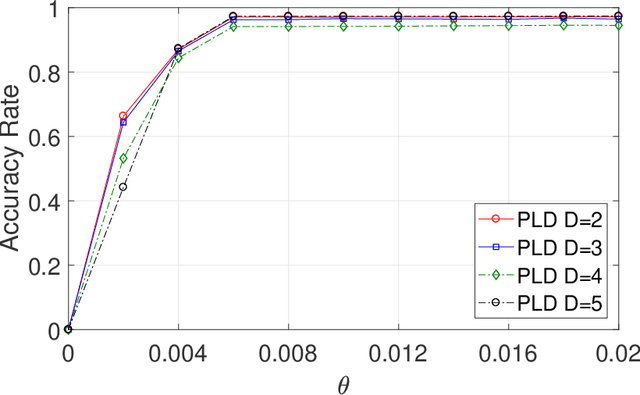
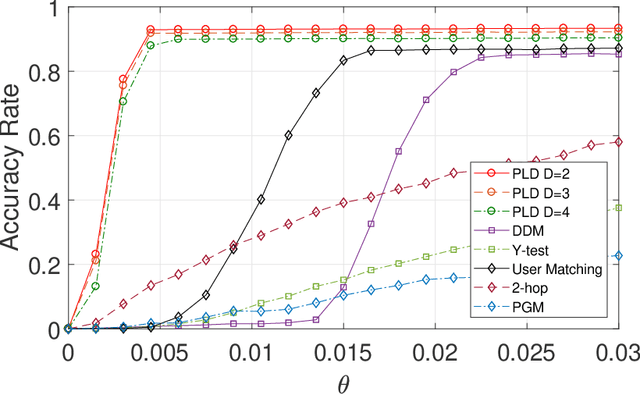
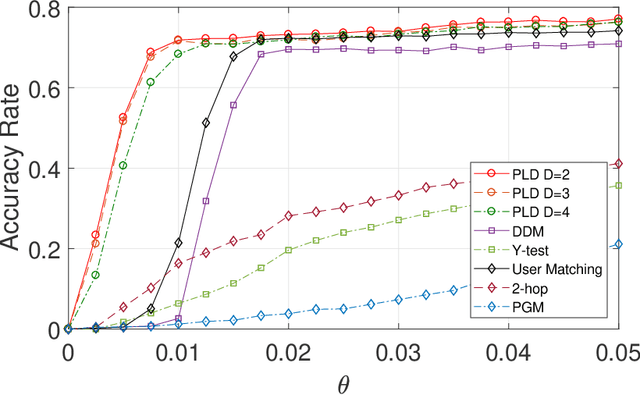
This paper studies seeded graph matching for power-law graphs. Assume that two edge-correlated graphs are independently edge-sampled from a common parent graph with a power-law degree distribution. A set of correctly matched vertex-pairs is chosen at random and revealed as initial seeds. Our goal is to use the seeds to recover the remaining latent vertex correspondence between the two graphs. Departing from the existing approaches that focus on the use of high-degree seeds in $1$-hop neighborhoods, we develop an efficient algorithm that exploits the low-degree seeds in suitably-defined $D$-hop neighborhoods. Specifically, we first match a set of vertex-pairs with appropriate degrees (which we refer to as the first slice) based on the number of low-degree seeds in their $D$-hop neighborhoods. This significantly reduces the number of initial seeds needed to trigger a cascading process to match the rest of the graphs. Under the Chung-Lu random graph model with $n$ vertices, max degree $\Theta(\sqrt{n})$, and the power-law exponent $2<\beta<3$, we show that as soon as $D> \frac{4-\beta}{3-\beta}$, by optimally choosing the first slice, with high probability our algorithm can correctly match a constant fraction of the true pairs without any error, provided with only $\Omega((\log n)^{4-\beta})$ initial seeds. Our result achieves an exponential reduction in the seed size requirement, as the best previously known result requires $n^{1/2+\epsilon}$ seeds (for any small constant $\epsilon>0$). Performance evaluation with synthetic and real data further corroborates the improved performance of our algorithm.

Graph Matching with Partially-Correct Seeds

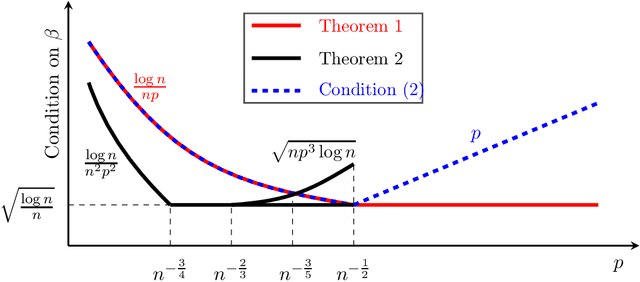
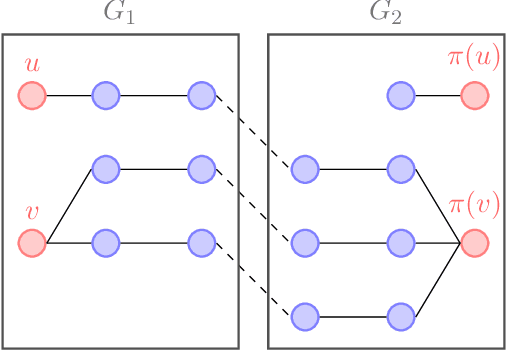
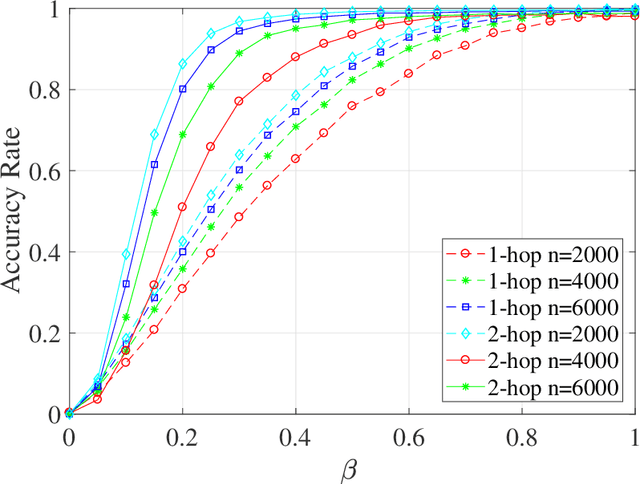
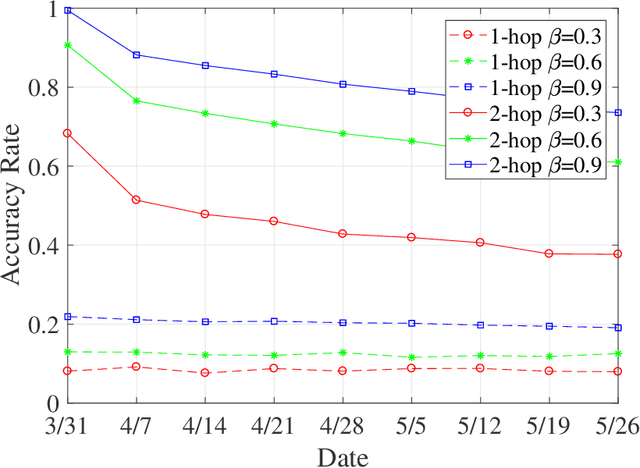
The graph matching problem aims to find the latent vertex correspondence between two edge-correlated graphs and has many practical applications. In this work, we study a version of the seeded graph matching problem, which assumes that a set of seeds, i.e., pre-mapped vertex-pairs, is given in advance. Specifically, consider two correlated graphs whose edges are sampled independently with probability $s$ from a parent \ER graph $\mathcal{G}(n,p)$. Furthermore, a mapping between the vertices of the two graphs is provided as seeds, of which an unknown $\beta$ fraction is correct. This problem was first studied in \cite{lubars2018correcting} where an algorithm is proposed and shown to perfectly recover the correct vertex mapping with high probability if $\beta\geq\max\left\{\frac{8}{3}p,\frac{16\log{n}}{nps^2}\right\}$. We improve their condition to $\beta\geq\max\left\{30\sqrt{\frac{\log n}{n(1-p)^2s^2}},\frac{45\log{n}}{np(1-p)^2s^2}\right)$. However, when $p=O\left( \sqrt{{\log n}/{ns^2}}\right)$, our improved condition still requires that $\beta$ must increase inversely proportional to $np$. In order to improve the matching performance for sparse graphs, we propose a new algorithm that uses "witnesses" in the 2-hop neighborhood, instead of only 1-hop neighborhood as in \cite{lubars2018correcting}. We show that when $np^2\leq\frac{1}{135\log n}$, our new algorithm can achieve perfect recovery with high probability if $\beta\geq\max\left\{900\sqrt{\frac{np^3(1-s)\log n}{s}},600\sqrt{\frac{\log n}{ns^4}}, \frac{1200\log n}{n^2p^2s^4}\right\}$ and $nps^2\geq 128\log n$. Numerical experiments on both synthetic and real graphs corroborate our theoretical findings and show that our 2-hop algorithm significantly outperforms the 1-hop algorithm when the graphs are relatively sparse.