SeedGNN: Graph Neural Networks for Supervised Seeded Graph Matching

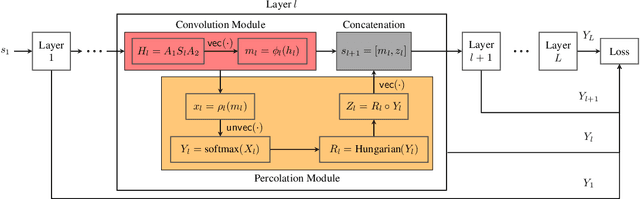
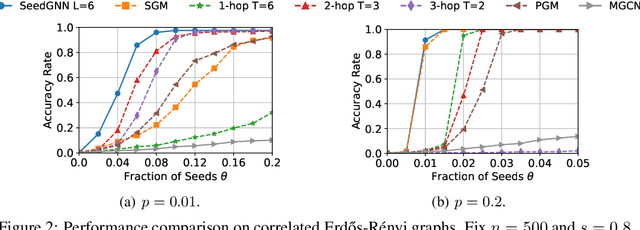
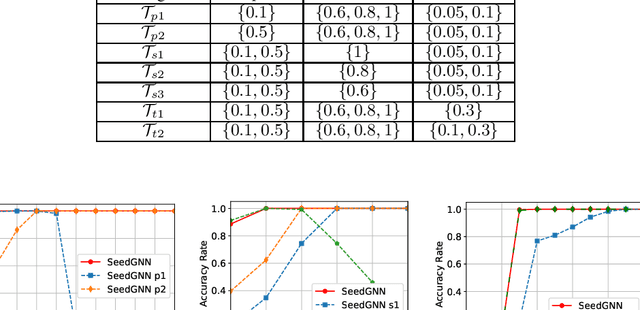
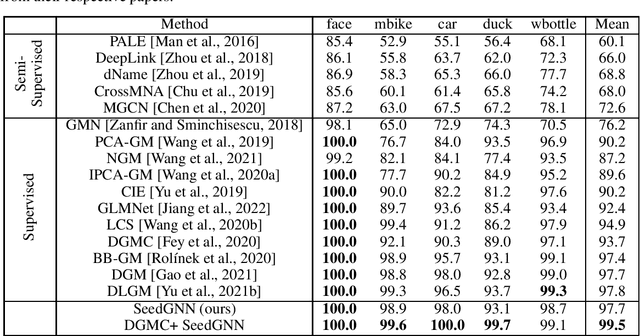
Recently, there have been significant interests in designing Graph Neural Networks (GNNs) for seeded graph matching, which aims to match two (unlabeled) graphs using only topological information and a small set of seeds. However, most previous GNN architectures for seeded graph matching employ a semi-supervised approach, which learns from only the seed set in a single pair of graphs, and therefore does not attempt to learn from many training examples/graphs to best match future unseen graphs. In contrast, this paper is the first to propose a supervised approach for seeded graph matching, which had so far only been used for seedless graph matching. Our proposed SeedGNN architecture employs a number of novel design choices that are inspired by theoretical studies of seeded graph matching. First, SeedGNN can easily learn the capability of counting and using witnesses of different hops, in a way that can be generalized to graphs with different sizes. Second, SeedGNN can use easily-matched pairs as new seeds to percolate and match other nodes. We evaluate SeedGNN on both synthetic and real graphs, and demonstrate significant performance improvement over both non-learning and learning algorithms in the existing literature. Further, our experiments confirm that the knowledge learned by SeedGNN from training graphs can be generalized to test graphs with different sizes and categories.

The Power of $D$-hops in Matching Power-Law Graphs

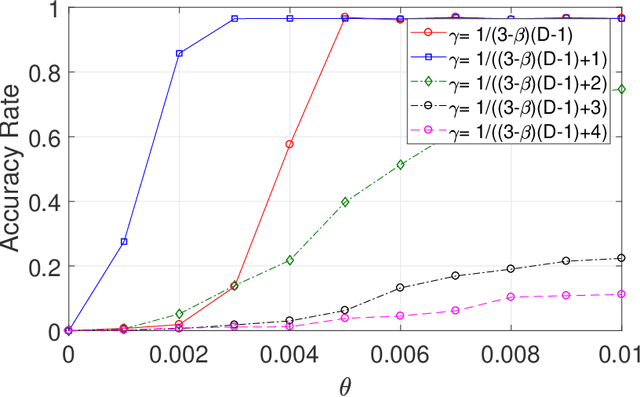
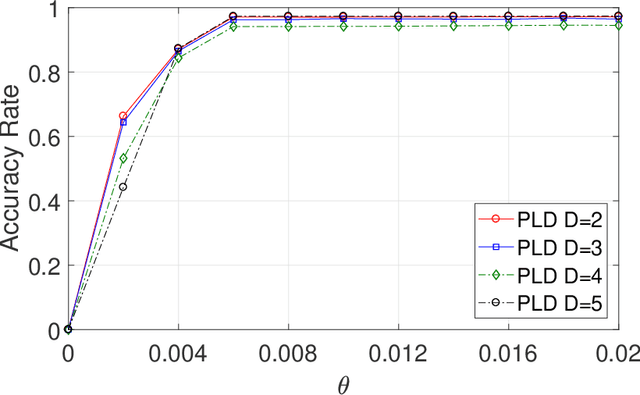
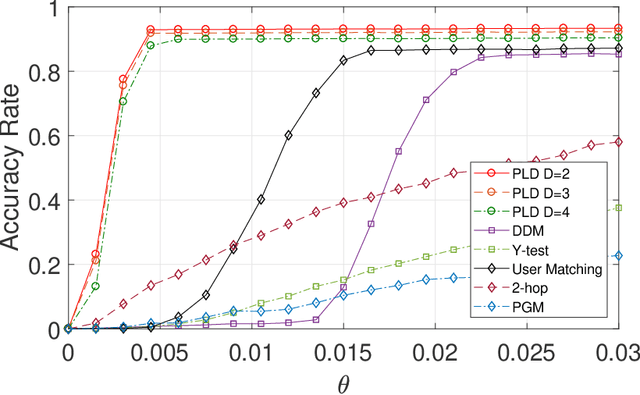
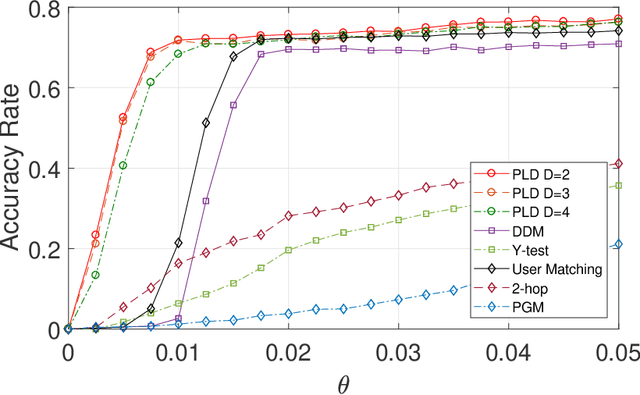
This paper studies seeded graph matching for power-law graphs. Assume that two edge-correlated graphs are independently edge-sampled from a common parent graph with a power-law degree distribution. A set of correctly matched vertex-pairs is chosen at random and revealed as initial seeds. Our goal is to use the seeds to recover the remaining latent vertex correspondence between the two graphs. Departing from the existing approaches that focus on the use of high-degree seeds in $1$-hop neighborhoods, we develop an efficient algorithm that exploits the low-degree seeds in suitably-defined $D$-hop neighborhoods. Specifically, we first match a set of vertex-pairs with appropriate degrees (which we refer to as the first slice) based on the number of low-degree seeds in their $D$-hop neighborhoods. This significantly reduces the number of initial seeds needed to trigger a cascading process to match the rest of the graphs. Under the Chung-Lu random graph model with $n$ vertices, max degree $\Theta(\sqrt{n})$, and the power-law exponent $2<\beta<3$, we show that as soon as $D> \frac{4-\beta}{3-\beta}$, by optimally choosing the first slice, with high probability our algorithm can correctly match a constant fraction of the true pairs without any error, provided with only $\Omega((\log n)^{4-\beta})$ initial seeds. Our result achieves an exponential reduction in the seed size requirement, as the best previously known result requires $n^{1/2+\epsilon}$ seeds (for any small constant $\epsilon>0$). Performance evaluation with synthetic and real data further corroborates the improved performance of our algorithm.

Graph Matching with Partially-Correct Seeds

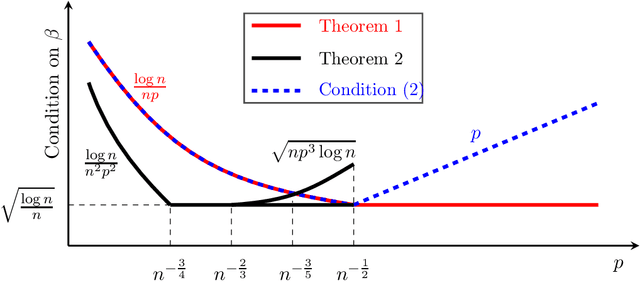
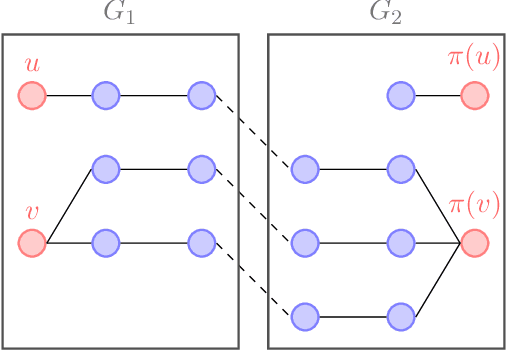
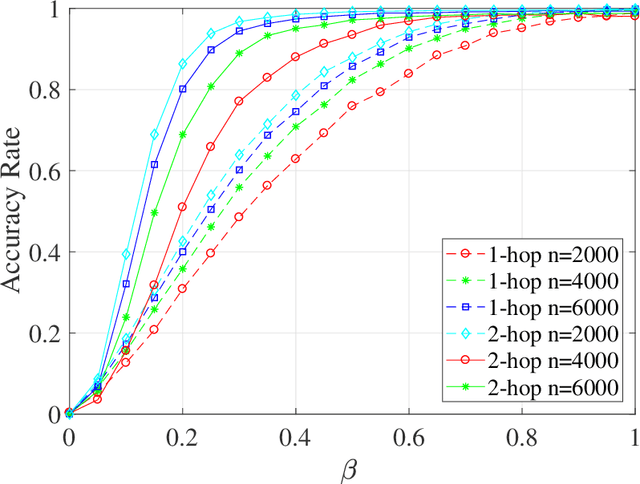
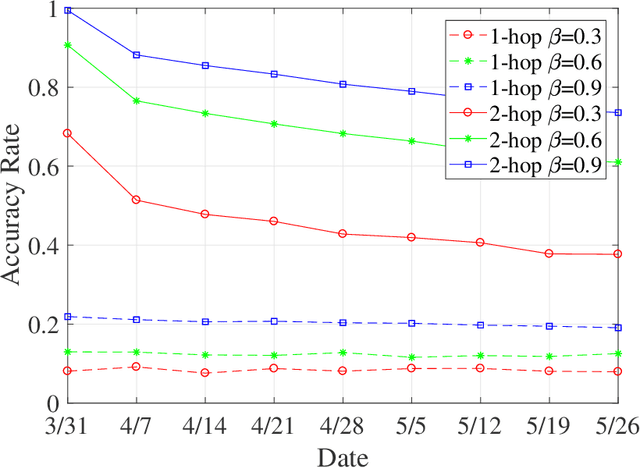
The graph matching problem aims to find the latent vertex correspondence between two edge-correlated graphs and has many practical applications. In this work, we study a version of the seeded graph matching problem, which assumes that a set of seeds, i.e., pre-mapped vertex-pairs, is given in advance. Specifically, consider two correlated graphs whose edges are sampled independently with probability $s$ from a parent \ER graph $\mathcal{G}(n,p)$. Furthermore, a mapping between the vertices of the two graphs is provided as seeds, of which an unknown $\beta$ fraction is correct. This problem was first studied in \cite{lubars2018correcting} where an algorithm is proposed and shown to perfectly recover the correct vertex mapping with high probability if $\beta\geq\max\left\{\frac{8}{3}p,\frac{16\log{n}}{nps^2}\right\}$. We improve their condition to $\beta\geq\max\left\{30\sqrt{\frac{\log n}{n(1-p)^2s^2}},\frac{45\log{n}}{np(1-p)^2s^2}\right)$. However, when $p=O\left( \sqrt{{\log n}/{ns^2}}\right)$, our improved condition still requires that $\beta$ must increase inversely proportional to $np$. In order to improve the matching performance for sparse graphs, we propose a new algorithm that uses "witnesses" in the 2-hop neighborhood, instead of only 1-hop neighborhood as in \cite{lubars2018correcting}. We show that when $np^2\leq\frac{1}{135\log n}$, our new algorithm can achieve perfect recovery with high probability if $\beta\geq\max\left\{900\sqrt{\frac{np^3(1-s)\log n}{s}},600\sqrt{\frac{\log n}{ns^4}}, \frac{1200\log n}{n^2p^2s^4}\right\}$ and $nps^2\geq 128\log n$. Numerical experiments on both synthetic and real graphs corroborate our theoretical findings and show that our 2-hop algorithm significantly outperforms the 1-hop algorithm when the graphs are relatively sparse.