Graph Matching with Partially-Correct Seeds
Paper and Code
Apr 08, 2020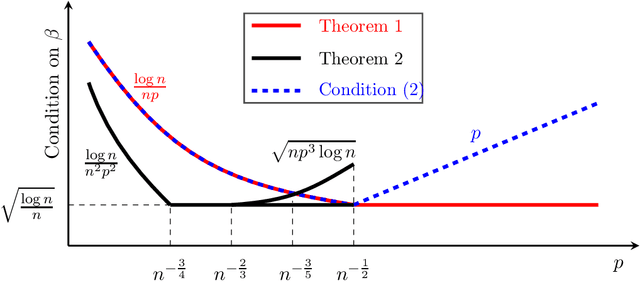
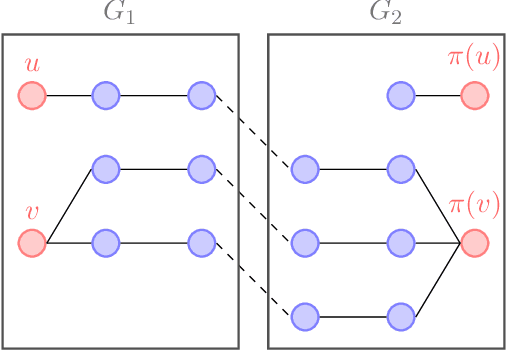
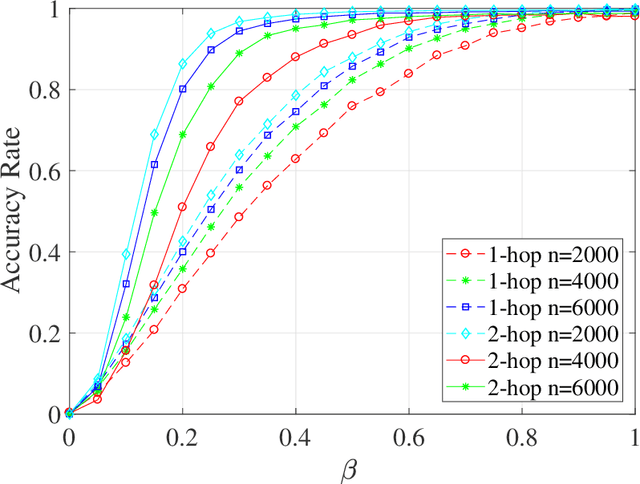
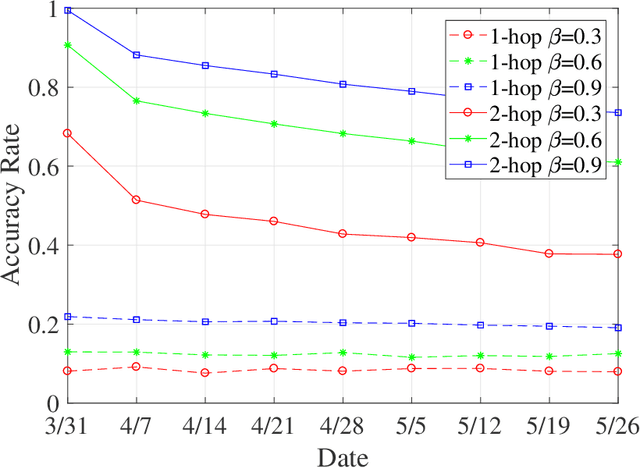
The graph matching problem aims to find the latent vertex correspondence between two edge-correlated graphs and has many practical applications. In this work, we study a version of the seeded graph matching problem, which assumes that a set of seeds, i.e., pre-mapped vertex-pairs, is given in advance. Specifically, consider two correlated graphs whose edges are sampled independently with probability $s$ from a parent \ER graph $\mathcal{G}(n,p)$. Furthermore, a mapping between the vertices of the two graphs is provided as seeds, of which an unknown $\beta$ fraction is correct. This problem was first studied in \cite{lubars2018correcting} where an algorithm is proposed and shown to perfectly recover the correct vertex mapping with high probability if $\beta\geq\max\left\{\frac{8}{3}p,\frac{16\log{n}}{nps^2}\right\}$. We improve their condition to $\beta\geq\max\left\{30\sqrt{\frac{\log n}{n(1-p)^2s^2}},\frac{45\log{n}}{np(1-p)^2s^2}\right)$. However, when $p=O\left( \sqrt{{\log n}/{ns^2}}\right)$, our improved condition still requires that $\beta$ must increase inversely proportional to $np$. In order to improve the matching performance for sparse graphs, we propose a new algorithm that uses "witnesses" in the 2-hop neighborhood, instead of only 1-hop neighborhood as in \cite{lubars2018correcting}. We show that when $np^2\leq\frac{1}{135\log n}$, our new algorithm can achieve perfect recovery with high probability if $\beta\geq\max\left\{900\sqrt{\frac{np^3(1-s)\log n}{s}},600\sqrt{\frac{\log n}{ns^4}}, \frac{1200\log n}{n^2p^2s^4}\right\}$ and $nps^2\geq 128\log n$. Numerical experiments on both synthetic and real graphs corroborate our theoretical findings and show that our 2-hop algorithm significantly outperforms the 1-hop algorithm when the graphs are relatively sparse.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge