Student-Teacher Learning from Clean Inputs to Noisy Inputs

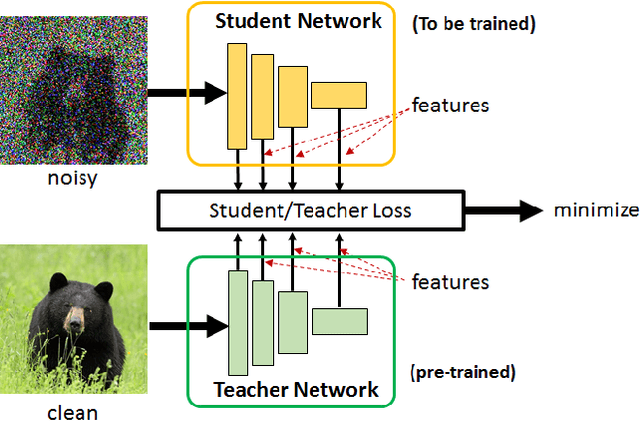
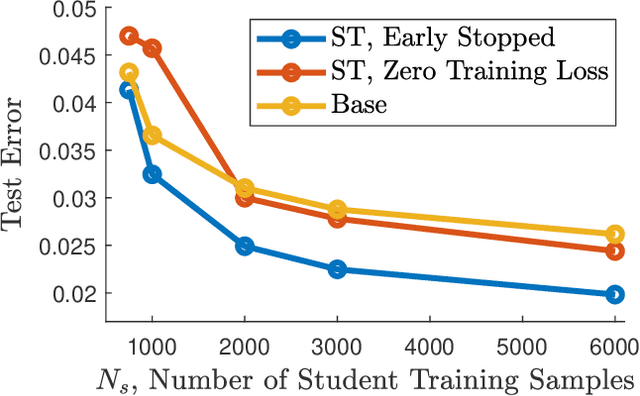
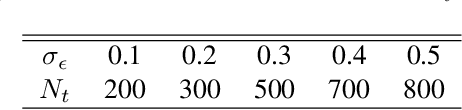
Feature-based student-teacher learning, a training method that encourages the student's hidden features to mimic those of the teacher network, is empirically successful in transferring the knowledge from a pre-trained teacher network to the student network. Furthermore, recent empirical results demonstrate that, the teacher's features can boost the student network's generalization even when the student's input sample is corrupted by noise. However, there is a lack of theoretical insights into why and when this method of transferring knowledge can be successful between such heterogeneous tasks. We analyze this method theoretically using deep linear networks, and experimentally using nonlinear networks. We identify three vital factors to the success of the method: (1) whether the student is trained to zero training loss; (2) how knowledgeable the teacher is on the clean-input problem; (3) how the teacher decomposes its knowledge in its hidden features. Lack of proper control in any of the three factors leads to failure of the student-teacher learning method.

Rethinking Atmospheric Turbulence Mitigation

State-of-the-art atmospheric turbulence image restoration methods utilize standard image processing tools such as optical flow, lucky region and blind deconvolution to restore the images. While promising results have been reported over the past decade, many of the methods are agnostic to the physical model that generates the distortion. In this paper, we revisit the turbulence restoration problem by analyzing the reference frame generation and the blind deconvolution steps in a typical restoration pipeline. By leveraging tools in large deviation theory, we rigorously prove the minimum number of frames required to generate a reliable reference for both static and dynamic scenes. We discuss how a turbulence agnostic model can lead to potential flaws, and how to configure a simple spatial-temporal non-local weighted averaging method to generate references. For blind deconvolution, we present a new data-driven prior by analyzing the distributions of the point spread functions. We demonstrate how a simple prior can outperform state-of-the-art blind deconvolution methods.