Vera Sacristán
Characterizing Universal Reconfigurability of Modular Pivoting Robots
Dec 14, 2020

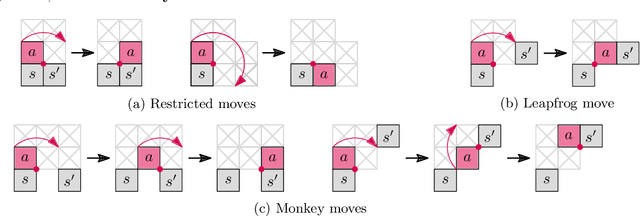

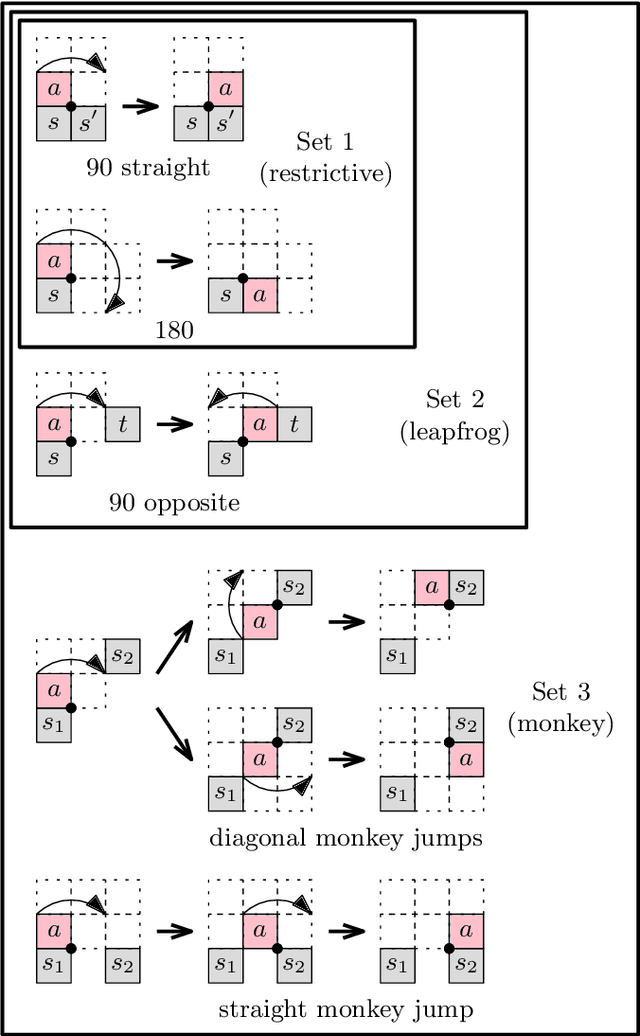
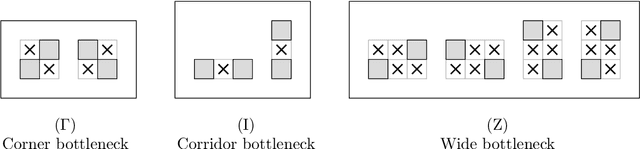
Abstract:We give both efficient algorithms and hardness results for reconfiguring between two connected configurations of modules in the hexagonal grid. The reconfiguration moves that we consider are "pivots", where a hexagonal module rotates around a vertex shared with another module. Following prior work on modular robots, we define two natural sets of hexagon pivoting moves of increasing power: restricted and monkey moves. When we allow both moves, we present the first universal reconfiguration algorithm, which transforms between any two connected configurations using $O(n^3)$ monkey moves. This result strongly contrasts the analogous problem for squares, where there are rigid examples that do not have a single pivoting move preserving connectivity. On the other hand, if we only allow restricted moves, we prove that the reconfiguration problem becomes PSPACE-complete. Moreover, we show that, in contrast to hexagons, the reconfiguration problem for pivoting squares is PSPACE-complete regardless of the set of pivoting moves allowed. In the process, we strengthen the reduction framework of Demaine et al. [FUN'18] that we consider of independent interest.
Universal Reconfiguration of Facet-Connected Modular Robots by Pivots: The $O(1)$ Musketeers
Sep 10, 2019

Abstract:We present the first universal reconfiguration algorithm for transforming a modular robot between any two facet-connected square-grid configurations using pivot moves. More precisely, we show that five extra "helper" modules ("musketeers") suffice to reconfigure the remaining $n$ modules between any two given configurations. Our algorithm uses $O(n^2)$ pivot moves, which is worst-case optimal. Previous reconfiguration algorithms either require less restrictive "sliding" moves, do not preserve facet-connectivity, or for the setting we consider, could only handle a small subset of configurations defined by a local forbidden pattern. Configurations with the forbidden pattern do have disconnected reconfiguration graphs (discrete configuration spaces), and indeed we show that they can have an exponential number of connected components. But forbidding the local pattern throughout the configuration is far from necessary, as we show that just a constant number of added modules (placed to be freely reconfigurable) suffice for universal reconfigurability. We also classify three different models of natural pivot moves that preserve facet-connectivity, and show separations between these models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge