Multidimensional Scaling: Approximation and Complexity

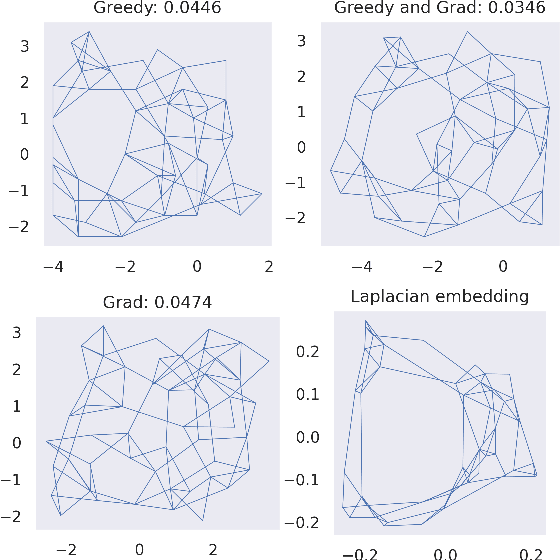
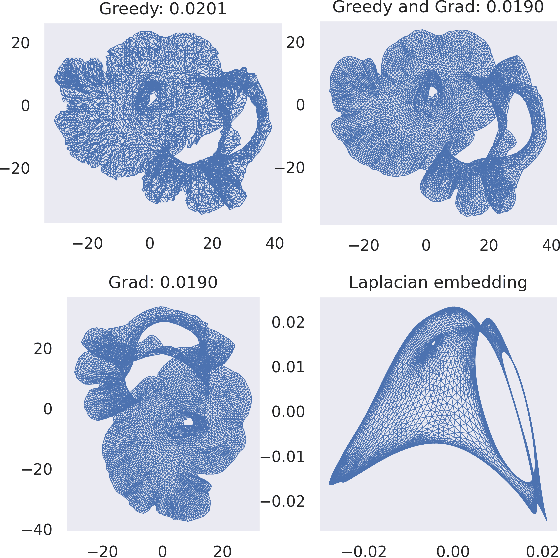
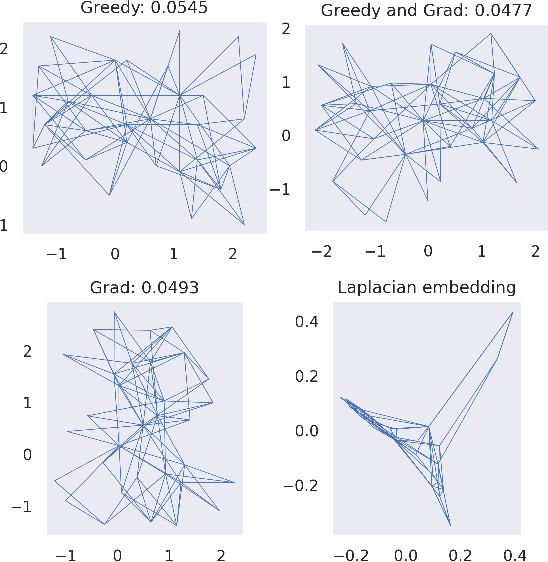
Metric Multidimensional scaling (MDS) is a classical method for generating meaningful (non-linear) low-dimensional embeddings of high-dimensional data. MDS has a long history in the statistics, machine learning, and graph drawing communities. In particular, the Kamada-Kawai force-directed graph drawing method is equivalent to MDS and is one of the most popular ways in practice to embed graphs into low dimensions. Despite its ubiquity, our theoretical understanding of MDS remains limited as its objective function is highly non-convex. In this paper, we prove that minimizing the Kamada-Kawai objective is NP-hard and give a provable approximation algorithm for optimizing it, which in particular is a PTAS on low-diameter graphs. We supplement this result with experiments suggesting possible connections between our greedy approximation algorithm and gradient-based methods.

Recursed is not Recursive: A Jarring Result

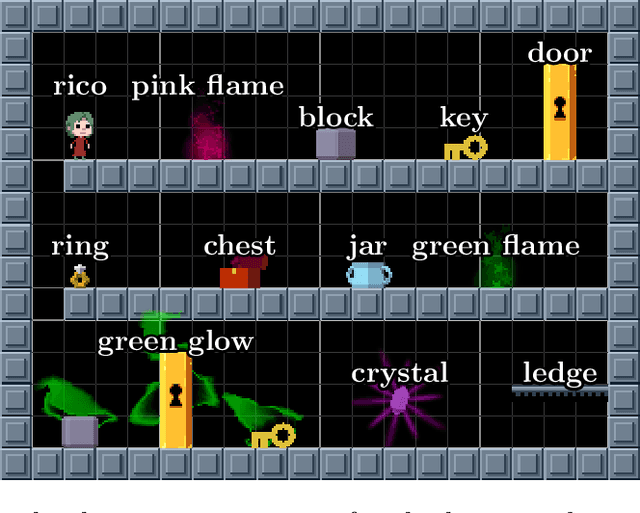
Recursed is a 2D puzzle platform video game featuring treasure chests that, when jumped into, instantiate a room that can later be exited (similar to function calls), optionally generating a \jar that returns back to that room (similar to continuations). We prove that Recursed is RE-complete and thus undecidable (not recursive) by a reduction from the Post Correspondence Problem. Our reduction is "practical": the reduction from PCP results in fully playable levels that abide by all constraints governing levels (including the 15x20 room size) designed for the main game. Our reduction is also "efficient": a Turing machine can be simulated by a Recursed level whose size is linear in the encoding size of the Turing machine and whose solution length is polynomial in the running time of the Turing machine.