Tackling the Problem of Distributional Shifts: Correcting Misspecified, High-Dimensional Data-Driven Priors for Inverse Problems

Bayesian inference for inverse problems hinges critically on the choice of priors. In the absence of specific prior information, population-level distributions can serve as effective priors for parameters of interest. With the advent of machine learning, the use of data-driven population-level distributions (encoded, e.g., in a trained deep neural network) as priors is emerging as an appealing alternative to simple parametric priors in a variety of inverse problems. However, in many astrophysical applications, it is often difficult or even impossible to acquire independent and identically distributed samples from the underlying data-generating process of interest to train these models. In these cases, corrupted data or a surrogate, e.g. a simulator, is often used to produce training samples, meaning that there is a risk of obtaining misspecified priors. This, in turn, can bias the inferred posteriors in ways that are difficult to quantify, which limits the potential applicability of these models in real-world scenarios. In this work, we propose addressing this issue by iteratively updating the population-level distributions by retraining the model with posterior samples from different sets of observations and showcase the potential of this method on the problem of background image reconstruction in strong gravitational lensing when score-based models are used as data-driven priors. We show that starting from a misspecified prior distribution, the updated distribution becomes progressively closer to the underlying population-level distribution, and the resulting posterior samples exhibit reduced bias after several updates.

Amortizing intractable inference in diffusion models for vision, language, and control

Diffusion models have emerged as effective distribution estimators in vision, language, and reinforcement learning, but their use as priors in downstream tasks poses an intractable posterior inference problem. This paper studies amortized sampling of the posterior over data, $\mathbf{x}\sim p^{\rm post}(\mathbf{x})\propto p(\mathbf{x})r(\mathbf{x})$, in a model that consists of a diffusion generative model prior $p(\mathbf{x})$ and a black-box constraint or likelihood function $r(\mathbf{x})$. We state and prove the asymptotic correctness of a data-free learning objective, relative trajectory balance, for training a diffusion model that samples from this posterior, a problem that existing methods solve only approximately or in restricted cases. Relative trajectory balance arises from the generative flow network perspective on diffusion models, which allows the use of deep reinforcement learning techniques to improve mode coverage. Experiments illustrate the broad potential of unbiased inference of arbitrary posteriors under diffusion priors: in vision (classifier guidance), language (infilling under a discrete diffusion LLM), and multimodal data (text-to-image generation). Beyond generative modeling, we apply relative trajectory balance to the problem of continuous control with a score-based behavior prior, achieving state-of-the-art results on benchmarks in offline reinforcement learning.

On diffusion models for amortized inference: Benchmarking and improving stochastic control and sampling

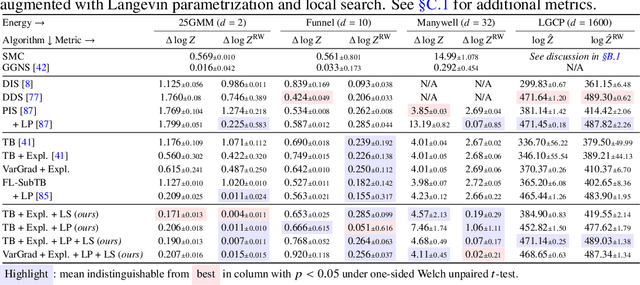
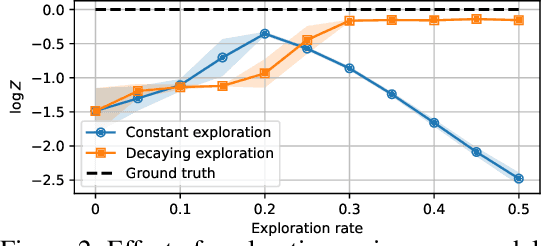
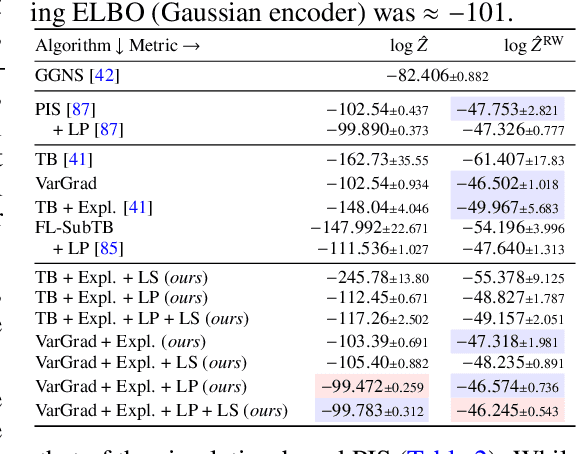
We study the problem of training diffusion models to sample from a distribution with a given unnormalized density or energy function. We benchmark several diffusion-structured inference methods, including simulation-based variational approaches and off-policy methods (continuous generative flow networks). Our results shed light on the relative advantages of existing algorithms while bringing into question some claims from past work. We also propose a novel exploration strategy for off-policy methods, based on local search in the target space with the use of a replay buffer, and show that it improves the quality of samples on a variety of target distributions. Our code for the sampling methods and benchmarks studied is made public at https://github.com/GFNOrg/gfn-diffusion as a base for future work on diffusion models for amortized inference.

Echoes in the Noise: Posterior Samples of Faint Galaxy Surface Brightness Profiles with Score-Based Likelihoods and Priors

Examining the detailed structure of galaxy populations provides valuable insights into their formation and evolution mechanisms. Significant barriers to such analysis are the non-trivial noise properties of real astronomical images and the point spread function (PSF) which blurs structure. Here we present a framework which combines recent advances in score-based likelihood characterization and diffusion model priors to perform a Bayesian analysis of image deconvolution. The method, when applied to minimally processed \emph{Hubble Space Telescope} (\emph{HST}) data, recovers structures which have otherwise only become visible in next-generation \emph{James Webb Space Telescope} (\emph{JWST}) imaging.

Bayesian Imaging for Radio Interferometry with Score-Based Priors

The inverse imaging task in radio interferometry is a key limiting factor to retrieving Bayesian uncertainties in radio astronomy in a computationally effective manner. We use a score-based prior derived from optical images of galaxies to recover images of protoplanetary disks from the DSHARP survey. We demonstrate that our method produces plausible posterior samples despite the misspecified galaxy prior. We show that our approach produces results which are competitive with existing radio interferometry imaging algorithms.

Pixelated Reconstruction of Foreground Density and Background Surface Brightness in Gravitational Lensing Systems using Recurrent Inference Machines

Modeling strong gravitational lenses in order to quantify the distortions in the images of background sources and to reconstruct the mass density in the foreground lenses has been a difficult computational challenge. As the quality of gravitational lens images increases, the task of fully exploiting the information they contain becomes computationally and algorithmically more difficult. In this work, we use a neural network based on the Recurrent Inference Machine (RIM) to simultaneously reconstruct an undistorted image of the background source and the lens mass density distribution as pixelated maps. The method iteratively reconstructs the model parameters (the image of the source and a pixelated density map) by learning the process of optimizing the likelihood given the data using the physical model (a ray-tracing simulation), regularized by a prior implicitly learned by the neural network through its training data. When compared to more traditional parametric models, the proposed method is significantly more expressive and can reconstruct complex mass distributions, which we demonstrate by using realistic lensing galaxies taken from the IllustrisTNG cosmological hydrodynamic simulation.

Posterior samples of source galaxies in strong gravitational lenses with score-based priors

Inferring accurate posteriors for high-dimensional representations of the brightness of gravitationally-lensed sources is a major challenge, in part due to the difficulties of accurately quantifying the priors. Here, we report the use of a score-based model to encode the prior for the inference of undistorted images of background galaxies. This model is trained on a set of high-resolution images of undistorted galaxies. By adding the likelihood score to the prior score and using a reverse-time stochastic differential equation solver, we obtain samples from the posterior. Our method produces independent posterior samples and models the data almost down to the noise level. We show how the balance between the likelihood and the prior meet our expectations in an experiment with out-of-distribution data.