Utility Theory for Sequential Decision Making
Paper and Code
Jun 27, 2022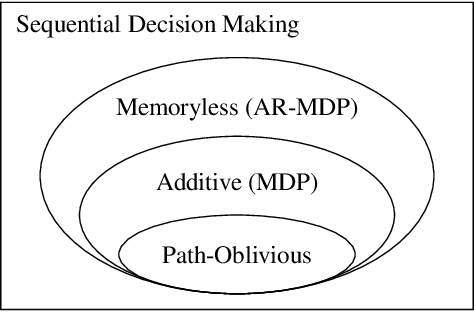
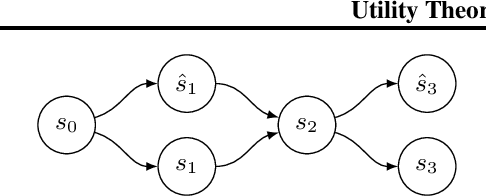
The von Neumann-Morgenstern (VNM) utility theorem shows that under certain axioms of rationality, decision-making is reduced to maximizing the expectation of some utility function. We extend these axioms to increasingly structured sequential decision making settings and identify the structure of the corresponding utility functions. In particular, we show that memoryless preferences lead to a utility in the form of a per transition reward and multiplicative factor on the future return. This result motivates a generalization of Markov Decision Processes (MDPs) with this structure on the agent's returns, which we call Affine-Reward MDPs. A stronger constraint on preferences is needed to recover the commonly used cumulative sum of scalar rewards in MDPs. A yet stronger constraint simplifies the utility function for goal-seeking agents in the form of a difference in some function of states that we call potential functions. Our necessary and sufficient conditions demystify the reward hypothesis that underlies the design of rational agents in reinforcement learning by adding an axiom to the VNM rationality axioms and motivates new directions for AI research involving sequential decision making.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge