Learning Broadcast Protocols

The problem of learning a computational model from examples has been receiving growing attention. Models of distributed systems are particularly challenging since they encompass an added succinctness. While positive results for learning some models of distributed systems have been obtained, so far the considered models assume a fixed number of processes interact. In this work we look for the first time (to the best of our knowledge) at the problem of learning a distributed system with an arbitrary number of processes, assuming only that there exists a cutoff. Specifically, we consider fine broadcast protocols, these are broadcast protocols (BPs) with a finite cutoff and no hidden states. We provide a learning algorithm that given a sample consistent with a fine BP, can infer a correct BP, with the help of an SMT solver. Moreover we show that the class of fine BPs is teachable, meaning that we can associate a finite set of words $\mathcal{S}_B$ with each BP $B$ in the class (a so-called characteristic set) so that the provided learning algorithm can correctly infer a correct BP from any consistent sample subsuming $\mathcal{S}_B$. On the negative size we show that (a) characteristic sets of exponential size are unavoidable, (b) the consistency problem for fine BPs is NP hard, and (c) fine BPs are not polynomially predictable.

Learning of Structurally Unambiguous Probabilistic Grammars

The problem of identifying a probabilistic context free grammar has two aspects: the first is determining the grammar's topology (the rules of the grammar) and the second is estimating probabilistic weights for each rule. Given the hardness results for learning context-free grammars in general, and probabilistic grammars in particular, most of the literature has concentrated on the second problem. In this work we address the first problem. We restrict attention to structurally unambiguous weighted context-free grammars (SUWCFG) and provide a query learning algorithm for \structurally unambiguous probabilistic context-free grammars (SUPCFG). We show that SUWCFG can be represented using \emph{co-linear multiplicity tree automata} (CMTA), and provide a polynomial learning algorithm that learns CMTAs. We show that the learned CMTA can be converted into a probabilistic grammar, thus providing a complete algorithm for learning a structurally unambiguous probabilistic context free grammar (both the grammar topology and the probabilistic weights) using structured membership queries and structured equivalence queries. A summarized version of this work was published at AAAI 21.

Safety Synthesis Sans Specification

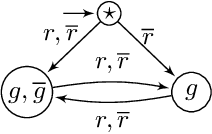
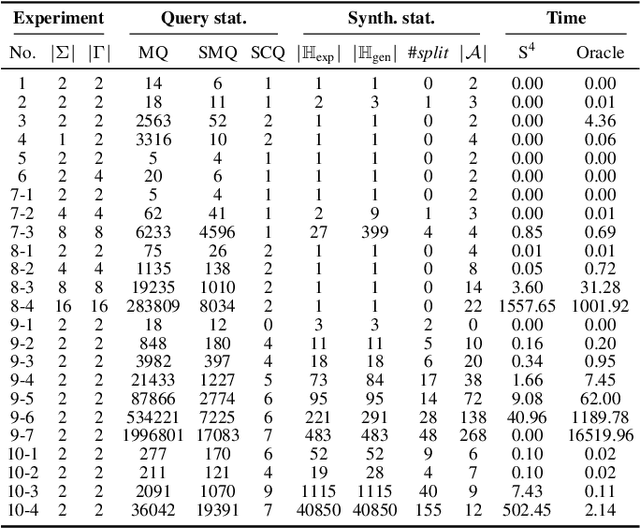
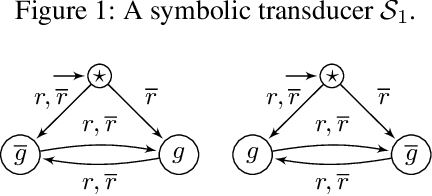
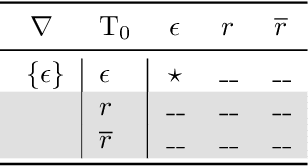
We define the problem of learning a transducer ${S}$ from a target language $U$ containing possibly conflicting transducers, using membership queries and conjecture queries. The requirement is that the language of ${S}$ be a subset of $U$. We argue that this is a natural question in many situations in hardware and software verification. We devise a learning algorithm for this problem and show that its time and query complexity is polynomial with respect to the rank of the target language, its incompatibility measure, and the maximal length of a given counterexample. We report on experiments conducted with a prototype implementation.

Inferring Symbolic Automata

We study the learnability of {symbolic finite state automata}, a model shown useful in many applications in software verification. The state-of-the-art literature on this topic follows the {query learning} paradigm, and so far all obtained results are positive. We provide a necessary condition for efficient learnability of SFAs in this paradigm, from which we obtain the first negative result. Most of this work studies learnability of SFAs under the paradigm of {identification in the limit using polynomial time and data}. We provide a sufficient condition for efficient learnability of SFAs in this paradigm, as well as a necessary condition, and provide several positive and negative results.

Learning Interpretable Models in the Property Specification Language

We address the problem of learning human-interpretable descriptions of a complex system from a finite set of positive and negative examples of its behavior. In contrast to most of the recent work in this area, which focuses on descriptions expressed in Linear Temporal Logic (LTL), we develop a learning algorithm for formulas in the IEEE standard temporal logic PSL (Property Specification Language). Our work is motivated by the fact that many natural properties, such as an event happening at every n-th point in time, cannot be expressed in LTL, whereas it is easy to express such properties in PSL. Moreover, formulas in PSL can be more succinct and easier to interpret (due to the use of regular expressions in PSL formulas) than formulas in LTL. Our learning algorithm builds on top of an existing algorithm for learning LTL formulas. Roughly speaking, our algorithm reduces the learning task to a constraint satisfaction problem in propositional logic and then uses a SAT solver to search for a solution in an incremental fashion. We have implemented our algorithm and performed a comparative study between the proposed method and the existing LTL learning algorithm. Our results illustrate the effectiveness of the proposed approach to provide succinct human-interpretable descriptions from examples.

Regular omega-Languages with an Informative Right Congruence

A regular language is almost fully characterized by its right congruence relation. Indeed, a regular language can always be recognized by a DFA isomorphic to the automaton corresponding to its right congruence, henceforth the Rightcon automaton. The same does not hold for regular omega-languages. The right congruence of a regular omega-language is not informative enough; many regular omega-languages have a trivial right congruence, and in general it is not always possible to define an omega-automaton recognizing a given language that is isomorphic to the rightcon automaton. The class of weak regular omega-languages does have an informative right congruence. That is, any weak regular omega-language can always be recognized by a deterministic B\"uchi automaton that is isomorphic to the rightcon automaton. Weak regular omega-languages reside in the lower levels of the expressiveness hierarchy of regular omega-languages. Are there more expressive sub-classes of regular omega languages that have an informative right congruence? Can we fully characterize the class of languages with a trivial right congruence? In this paper we try to place some additional pieces of this big puzzle.

SyGuS-Comp 2017: Results and Analysis

Syntax-Guided Synthesis (SyGuS) is the computational problem of finding an implementation f that meets both a semantic constraint given by a logical formula phi in a background theory T, and a syntactic constraint given by a grammar G, which specifies the allowed set of candidate implementations. Such a synthesis problem can be formally defined in SyGuS-IF, a language that is built on top of SMT-LIB. The Syntax-Guided Synthesis Competition (SyGuS-Comp) is an effort to facilitate, bring together and accelerate research and development of efficient solvers for SyGuS by providing a platform for evaluating different synthesis techniques on a comprehensive set of benchmarks. In this year's competition six new solvers competed on over 1500 benchmarks. This paper presents and analyses the results of SyGuS-Comp'17.

SyGuS-Comp 2016: Results and Analysis

Syntax-Guided Synthesis (SyGuS) is the computational problem of finding an implementation f that meets both a semantic constraint given by a logical formula $\varphi$ in a background theory T, and a syntactic constraint given by a grammar G, which specifies the allowed set of candidate implementations. Such a synthesis problem can be formally defined in SyGuS-IF, a language that is built on top of SMT-LIB. The Syntax-Guided Synthesis Competition (SyGuS-Comp) is an effort to facilitate, bring together and accelerate research and development of efficient solvers for SyGuS by providing a platform for evaluating different synthesis techniques on a comprehensive set of benchmarks. In this year's competition we added a new track devoted to programming by examples. This track consisted of two categories, one using the theory of bit-vectors and one using the theory of strings. This paper presents and analyses the results of SyGuS-Comp'16.