On the Semantics of Primary Cause in Hybrid Dynamic Domains

Reasoning about actual causes of observed effects is fundamental to the study of rationality. This important problem has been studied since the time of Aristotle, with formal mathematical accounts emerging recently. We live in a world where change due to actions can be both discrete and continuous, that is, hybrid. Yet, despite extensive research on actual causation, only few recent studies looked into causation with continuous change. Building on recent progress, in this paper we propose two definitions of primary cause in a hybrid action-theoretic framework, namely the hybrid temporal situation calculus. One of these is foundational in nature while the other formalizes causation through contributions, which can then be verified from a counterfactual perspective using a modified ``but-for'' test. We prove that these two definitions are indeed equivalent. We then show that our definitions of causation have some intuitively justifiable properties.

Learning Half-Spaces from Perturbed Contrastive Examples

We study learning under a two-step contrastive example oracle, as introduced by Mansouri et. al. (2025), where each queried (or sampled) labeled example is paired with an additional contrastive example of opposite label. While Mansouri et al. assume an idealized setting, where the contrastive example is at minimum distance of the originally queried/sampled point, we introduce and analyze a mechanism, parameterized by a non-decreasing noise function $f$, under which this ideal contrastive example is perturbed. The amount of perturbation is controlled by $f(d)$, where $d$ is the distance of the queried/sampled point to the decision boundary. Intuitively, this results in higher-quality contrastive examples for points closer to the decision boundary. We study this model in two settings: (i) when the maximum perturbation magnitude is fixed, and (ii) when it is stochastic. For one-dimensional thresholds and for half-spaces under the uniform distribution on a bounded domain, we characterize active and passive contrastive sample complexity in dependence on the function $f$. We show that, under certain conditions on $f$, the presence of contrastive examples speeds up learning in terms of asymptotic query complexity and asymptotic expected query complexity.

Common Benchmarks Undervalue the Generalization Power of Programmatic Policies

Algorithms for learning programmatic representations for sequential decision-making problems are often evaluated on out-of-distribution (OOD) problems, with the common conclusion that programmatic policies generalize better than neural policies on OOD problems. In this position paper, we argue that commonly used benchmarks undervalue the generalization capabilities of programmatic representations. We analyze the experiments of four papers from the literature and show that neural policies, which were shown not to generalize, can generalize as effectively as programmatic policies on OOD problems. This is achieved with simple changes in the neural policies training pipeline. Namely, we show that simpler neural architectures with the same type of sparse observation used with programmatic policies can help attain OOD generalization. Another modification we have shown to be effective is the use of reward functions that allow for safer policies (e.g., agents that drive slowly can generalize better). Also, we argue for creating benchmark problems highlighting concepts needed for OOD generalization that may challenge neural policies but align with programmatic representations, such as tasks requiring algorithmic constructs like stacks.

Approximation Algorithms for Preference Aggregation Using CP-Nets

This paper studies the design and analysis of approximation algorithms for aggregating preferences over combinatorial domains, represented using Conditional Preference Networks (CP-nets). Its focus is on aggregating preferences over so-called \emph{swaps}, for which optimal solutions in general are already known to be of exponential size. We first analyze a trivial 2-approximation algorithm that simply outputs the best of the given input preferences, and establish a structural condition under which the approximation ratio of this algorithm is improved to $4/3$. We then propose a polynomial-time approximation algorithm whose outputs are provably no worse than those of the trivial algorithm, but often substantially better. A family of problem instances is presented for which our improved algorithm produces optimal solutions, while, for any $\varepsilon$, the trivial algorithm can\emph{not}\/ attain a $(2-\varepsilon)$-approximation. These results may lead to the first polynomial-time approximation algorithm that solves the CP-net aggregation problem for swaps with an approximation ratio substantially better than $2$.

A Labelled Sample Compression Scheme of Size at Most Quadratic in the VC Dimension

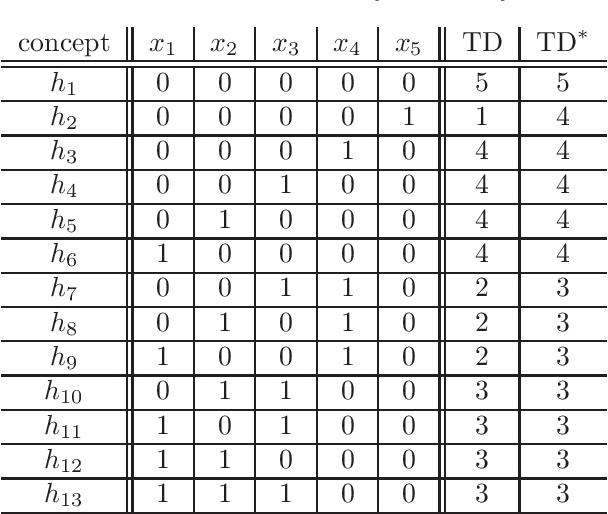
This paper presents a construction of a proper and stable labelled sample compression scheme of size $O(\VCD^2)$ for any finite concept class, where $\VCD$ denotes the Vapnik-Chervonenkis Dimension. The construction is based on a well-known model of machine teaching, referred to as recursive teaching dimension. This substantially improves on the currently best known bound on the size of sample compression schemes (due to Moran and Yehudayoff), which is exponential in $\VCD$. The long-standing open question whether the smallest size of a sample compression scheme is in $O(\VCD)$ remains unresolved, but our results show that research on machine teaching is a promising avenue for the study of this open problem. As further evidence of the strong connections between machine teaching and sample compression, we prove that the model of no-clash teaching, introduced by Kirkpatrick et al., can be used to define a non-trivial lower bound on the size of stable sample compression schemes.

Actively Learning Deep Neural Networks with Uncertainty Sampling Based on Sum-Product Networks

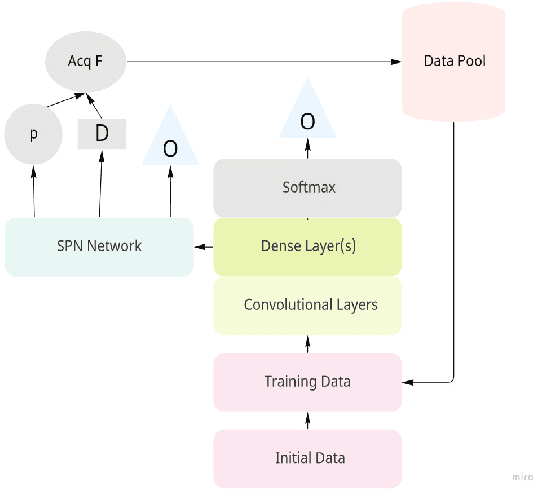
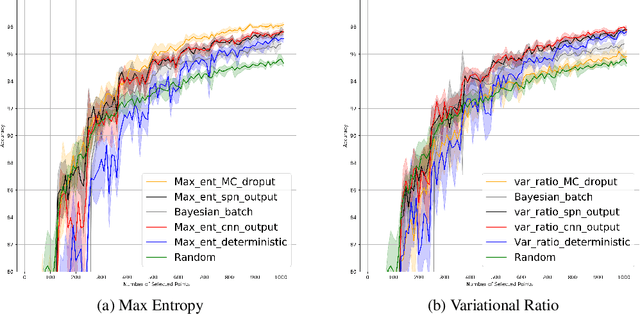
Active learning is popular approach for reducing the amount of data in training deep neural network model. Its success hinges on the choice of an effective acquisition function, which ranks not yet labeled data points according to their expected informativeness. In uncertainty sampling, the uncertainty that the current model has about a point's class label is the main criterion for this type of ranking. This paper proposes a new approach to uncertainty sampling in training a Convolutional Neural Network (CNN). The main idea is to use feature representation extracted extracted by the CNN as data for training a Sum-Product Network (SPN). Since SPNs are typically used for estimating the distribution of a dataset, they are well suited to the task of estimating class probabilities that can be used directly by standard acquisition functions such as max entropy and variational ratio. Moreover, we enhance these acquisition functions by weights calculated with the help of the SPN model; these weights make the acquisition function more sensitive to the diversity of conceivable class labels for data points. The effectiveness of our method is demonstrated in an experimental study on the MNIST, Fashion-MNIST and CIFAR-10 datasets, where we compare it to the state-of-the-art methods MC Dropout and Bayesian Batch.

Inferring Symbolic Automata

We study the learnability of {symbolic finite state automata}, a model shown useful in many applications in software verification. The state-of-the-art literature on this topic follows the {query learning} paradigm, and so far all obtained results are positive. We provide a necessary condition for efficient learnability of SFAs in this paradigm, from which we obtain the first negative result. Most of this work studies learnability of SFAs under the paradigm of {identification in the limit using polynomial time and data}. We provide a sufficient condition for efficient learnability of SFAs in this paradigm, as well as a necessary condition, and provide several positive and negative results.

Optimal Collusion-Free Teaching

Formal models of learning from teachers need to respect certain criteria to avoid collusion. The most commonly accepted notion of collusion-freeness was proposed by Goldman and Mathias (1996), and various teaching models obeying their criterion have been studied. For each model $M$ and each concept class $\mathcal{C}$, a parameter $M$-$\mathrm{TD}(\mathcal{C})$ refers to the teaching dimension of concept class $\mathcal{C}$ in model $M$---defined to be the number of examples required for teaching a concept, in the worst case over all concepts in $\mathcal{C}$. This paper introduces a new model of teaching, called no-clash teaching, together with the corresponding parameter $\mathrm{NCTD}(\mathcal{C})$. No-clash teaching is provably optimal in the strong sense that, given any concept class $\mathcal{C}$ and any model $M$ obeying Goldman and Mathias's collusion-freeness criterion, one obtains $\mathrm{NCTD}(\mathcal{C})\le M$-$\mathrm{TD}(\mathcal{C})$. We also study a corresponding notion $\mathrm{NCTD}^+$ for the case of learning from positive data only, establish useful bounds on $\mathrm{NCTD}$ and $\mathrm{NCTD}^+$, and discuss relations of these parameters to the VC-dimension and to sample compression. In addition to formulating an optimal model of collusion-free teaching, our main results are on the computational complexity of deciding whether $\mathrm{NCTD}^+(\mathcal{C})=k$ (or $\mathrm{NCTD}(\mathcal{C})=k$) for given $\mathcal{C}$ and $k$. We show some such decision problems to be equivalent to the existence question for certain constrained matchings in bipartite graphs. Our NP-hardness results for the latter are of independent interest in the study of constrained graph matchings.

The Complexity of Learning Acyclic Conditional Preference Networks

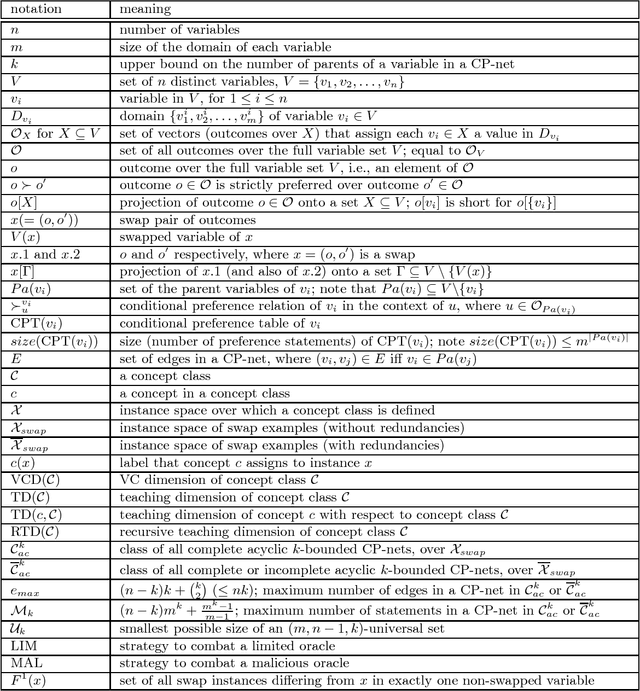
Learning of user preferences, as represented by, for example, Conditional Preference Networks (CP-nets), has become a core issue in AI research. Recent studies investigate learning of CP-nets from randomly chosen examples or from membership and equivalence queries. To assess the optimality of learning algorithms as well as to better understand the combinatorial structure of classes of CP-nets, it is helpful to calculate certain learning-theoretic information complexity parameters. This article focuses on the frequently studied case of learning from so-called swap examples, which express preferences among objects that differ in only one attribute. It presents bounds on or exact values of some well-studied information complexity parameters, namely the VC dimension, the teaching dimension, and the recursive teaching dimension, for classes of acyclic CP-nets. We further provide algorithms that learn tree-structured and general acyclic CP-nets from membership queries. Using our results on complexity parameters, we assess the optimality of our algorithms as well as that of another query learning algorithm for acyclic CP-nets presented in the literature. Our algorithms are near-optimal, and can, under certain assumptions, be adapted to the case when the membership oracle is faulty.

An Overview of Machine Teaching

In this paper we try to organize machine teaching as a coherent set of ideas. Each idea is presented as varying along a dimension. The collection of dimensions then form the problem space of machine teaching, such that existing teaching problems can be characterized in this space. We hope this organization allows us to gain deeper understanding of individual teaching problems, discover connections among them, and identify gaps in the field.