A Labelled Sample Compression Scheme of Size at Most Quadratic in the VC Dimension

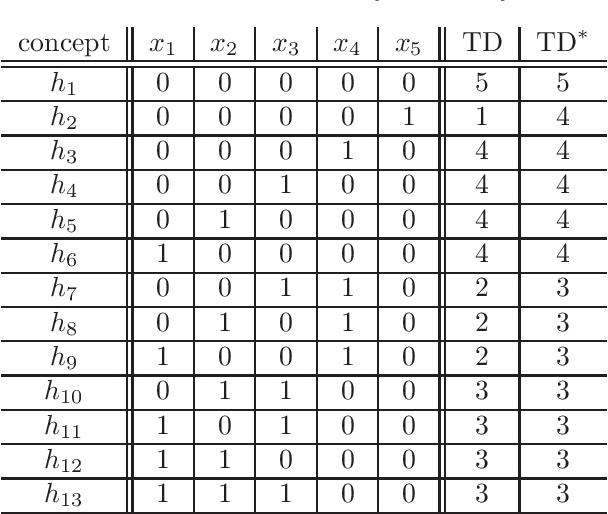
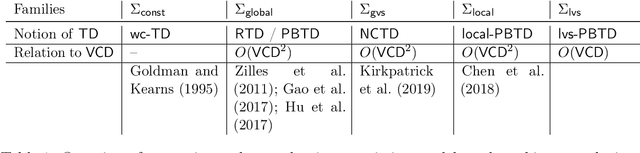
This paper presents a construction of a proper and stable labelled sample compression scheme of size $O(\VCD^2)$ for any finite concept class, where $\VCD$ denotes the Vapnik-Chervonenkis Dimension. The construction is based on a well-known model of machine teaching, referred to as recursive teaching dimension. This substantially improves on the currently best known bound on the size of sample compression schemes (due to Moran and Yehudayoff), which is exponential in $\VCD$. The long-standing open question whether the smallest size of a sample compression scheme is in $O(\VCD)$ remains unresolved, but our results show that research on machine teaching is a promising avenue for the study of this open problem. As further evidence of the strong connections between machine teaching and sample compression, we prove that the model of no-clash teaching, introduced by Kirkpatrick et al., can be used to define a non-trivial lower bound on the size of stable sample compression schemes.

Deep Reinforcement Learning for Online Control of Stochastic Partial Differential Equations

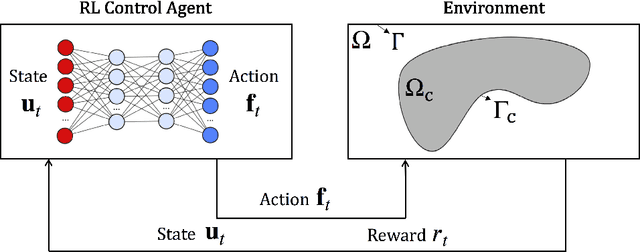
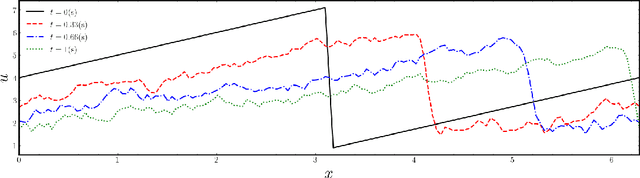
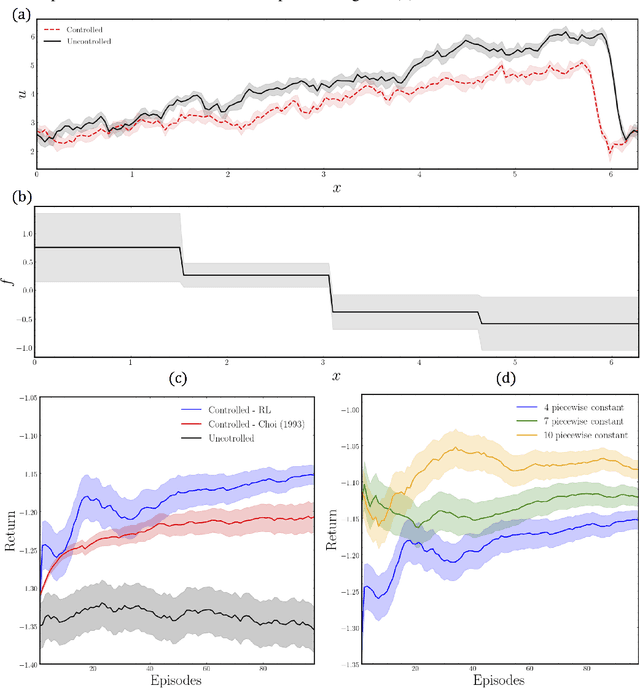
In many areas, such as the physical sciences, life sciences, and finance, control approaches are used to achieve a desired goal in complex dynamical systems governed by differential equations. In this work we formulate the problem of controlling stochastic partial differential equations (SPDE) as a reinforcement learning problem. We present a learning-based, distributed control approach for online control of a system of SPDEs with high dimensional state-action space using deep deterministic policy gradient method. We tested the performance of our method on the problem of controlling the stochastic Burgers' equation, describing a turbulent fluid flow in an infinitely large domain.

Preference-Based Batch and Sequential Teaching

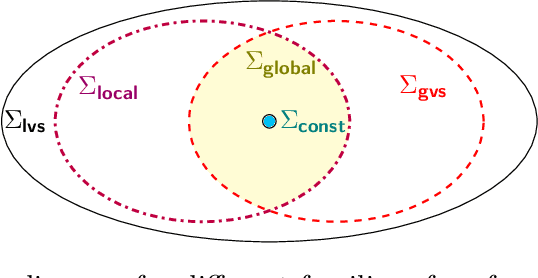
Algorithmic machine teaching studies the interaction between a teacher and a learner where the teacher selects labeled examples aiming at teaching a target hypothesis. In a quest to lower teaching complexity, several teaching models and complexity measures have been proposed for both the batch settings (e.g., worst-case, recursive, preference-based, and non-clashing models) and the sequential settings (e.g., local preference-based model). To better understand the connections between these models, we develop a novel framework that captures the teaching process via preference functions $\Sigma$. In our framework, each function $\sigma \in \Sigma$ induces a teacher-learner pair with teaching complexity as $TD(\sigma)$. We show that the above-mentioned teaching models are equivalent to specific types/families of preference functions. We analyze several properties of the teaching complexity parameter $TD(\sigma)$ associated with different families of the preference functions, e.g., comparison to the VC dimension of the hypothesis class and additivity/sub-additivity of $TD(\sigma)$ over disjoint domains. Finally, we identify preference functions inducing a novel family of sequential models with teaching complexity linear in the VC dimension: this is in contrast to the best-known complexity result for the batch models, which is quadratic in the VC dimension.

Understanding the Power and Limitations of Teaching with Imperfect Knowledge

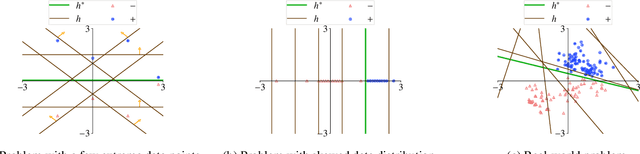
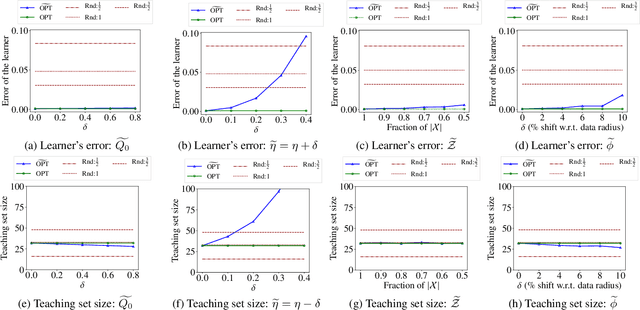
Machine teaching studies the interaction between a teacher and a student/learner where the teacher selects training examples for the learner to learn a specific task. The typical assumption is that the teacher has perfect knowledge of the task---this knowledge comprises knowing the desired learning target, having the exact task representation used by the learner, and knowing the parameters capturing the learning dynamics of the learner. Inspired by real-world applications of machine teaching in education, we consider the setting where teacher's knowledge is limited and noisy, and the key research question we study is the following: When does a teacher succeed or fail in effectively teaching a learner using its imperfect knowledge? We answer this question by showing connections to how imperfect knowledge affects the teacher's solution of the corresponding machine teaching problem when constructing optimal teaching sets. Our results have important implications for designing robust teaching algorithms for real-world applications.

Preference-Based Batch and Sequential Teaching: Towards a Unified View of Models

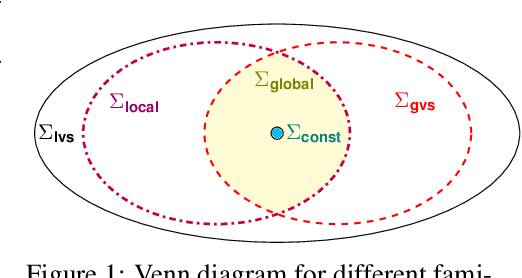
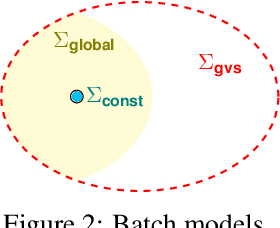
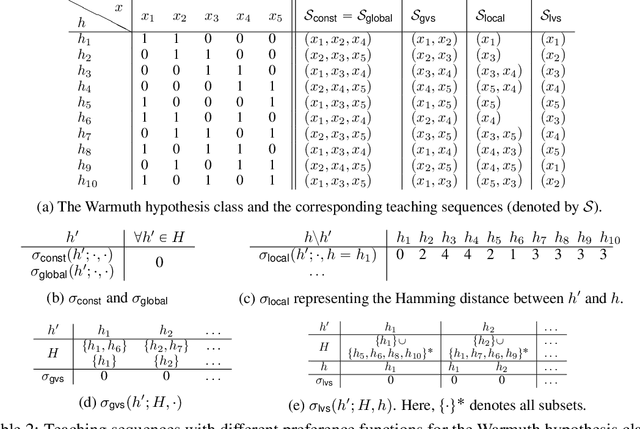
Algorithmic machine teaching studies the interaction between a teacher and a learner where the teacher selects labeled examples aiming at teaching a target hypothesis. In a quest to lower teaching complexity and to achieve more natural teacher-learner interactions, several teaching models and complexity measures have been proposed for both the batch settings (e.g., worst-case, recursive, preference-based, and non-clashing models) as well as the sequential settings (e.g., local preference-based model). To better understand the connections between these different batch and sequential models, we develop a novel framework which captures the teaching process via preference functions $\Sigma$. In our framework, each function $\sigma \in \Sigma$ induces a teacher-learner pair with teaching complexity as $\TD(\sigma)$. We show that the above-mentioned teaching models are equivalent to specific types/families of preference functions in our framework. This equivalence, in turn, allows us to study the differences between two important teaching models, namely $\sigma$ functions inducing the strongest batch (i.e., non-clashing) model and $\sigma$ functions inducing a weak sequential (i.e., local preference-based) model. Finally, we identify preference functions inducing a novel family of sequential models with teaching complexity linear in the VC dimension of the hypothesis class: this is in contrast to the best known complexity result for the batch models which is quadratic in the VC dimension.

ChOracle: A Unified Statistical Framework for Churn Prediction

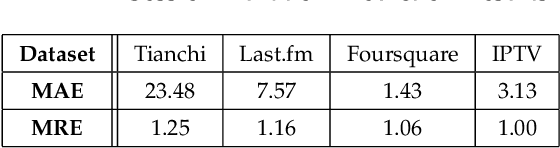
User churn is an important issue in online services that threatens the health and profitability of services. Most of the previous works on churn prediction convert the problem into a binary classification task where the users are labeled as churned and non-churned. More recently, some works have tried to convert the user churn prediction problem into the prediction of user return time. In this approach which is more realistic in real world online services, at each time-step the model predicts the user return time instead of predicting a churn label. However, the previous works in this category suffer from lack of generality and require high computational complexity. In this paper, we introduce \emph{ChOracle}, an oracle that predicts the user churn by modeling the user return times to service by utilizing a combination of Temporal Point Processes and Recurrent Neural Networks. Moreover, we incorporate latent variables into the proposed recurrent neural network to model the latent user loyalty to the system. We also develop an efficient approximate variational algorithm for learning parameters of the proposed RNN by using back propagation through time. Finally, we demonstrate the superior performance of ChOracle on a wide variety of real world datasets.