Learning interactions to boost human creativity with bandits and GPT-4

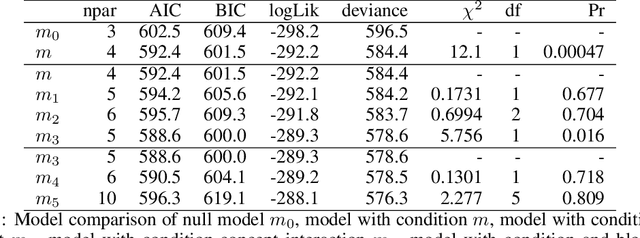
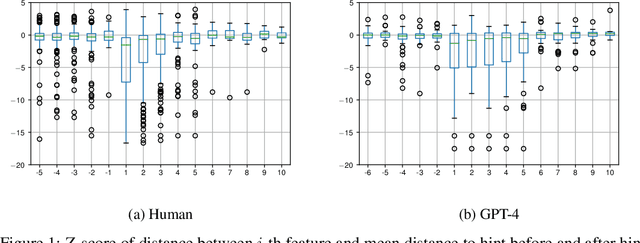
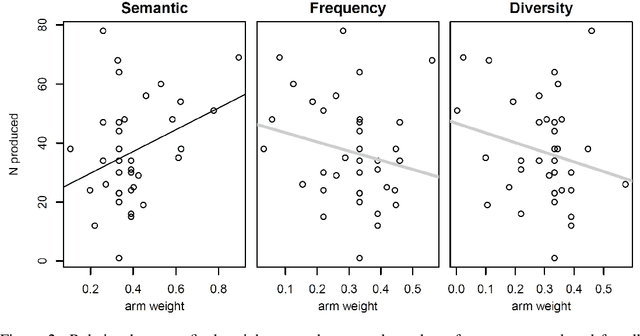
This paper considers how interactions with AI algorithms can boost human creative thought. We employ a psychological task that demonstrates limits on human creativity, namely semantic feature generation: given a concept name, respondents must list as many of its features as possible. Human participants typically produce only a fraction of the features they know before getting "stuck." In experiments with humans and with a language AI (GPT-4) we contrast behavior in the standard task versus a variant in which participants can ask for algorithmically-generated hints. Algorithm choice is administered by a multi-armed bandit whose reward indicates whether the hint helped generating more features. Humans and the AI show similar benefits from hints, and remarkably, bandits learning from AI responses prefer the same prompting strategy as those learning from human behavior. The results suggest that strategies for boosting human creativity via computer interactions can be learned by bandits run on groups of simulated participants.

Training-Time Attacks against k-Nearest Neighbors

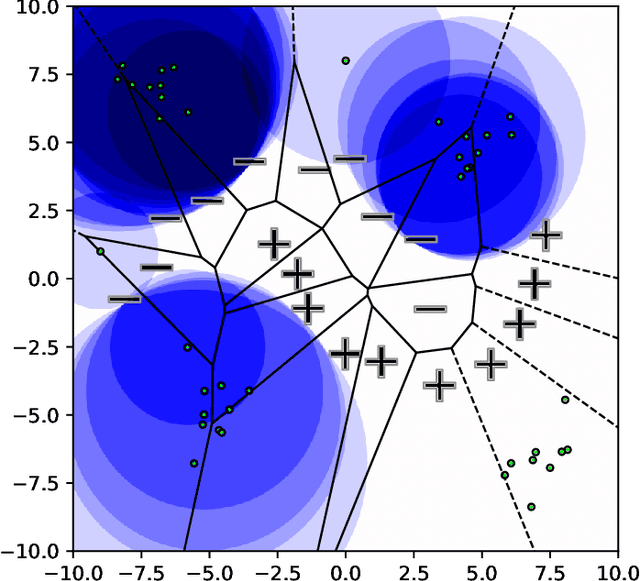
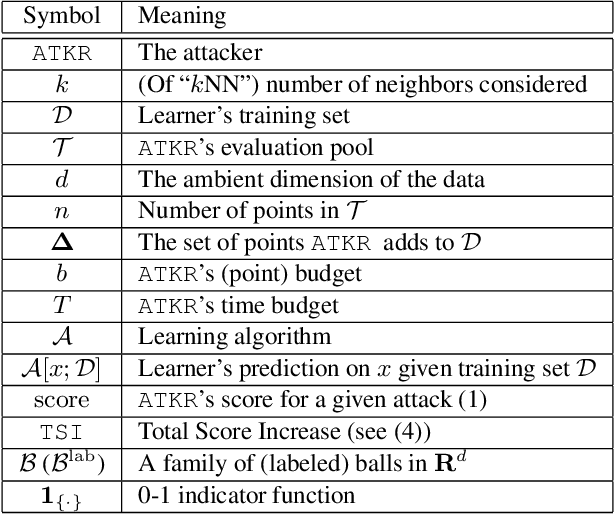
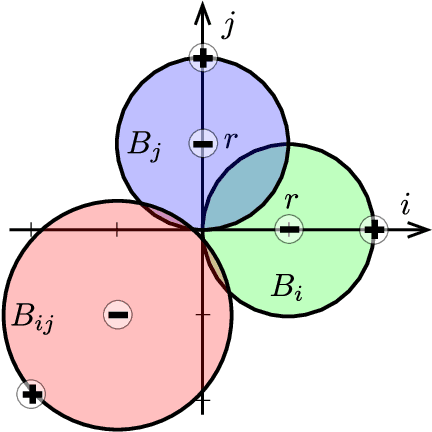
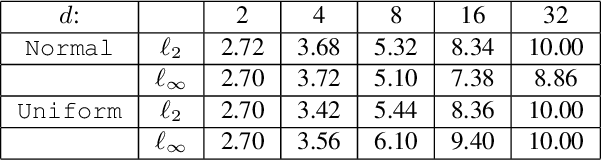
Nearest neighbor-based methods are commonly used for classification tasks and as subroutines of other data-analysis methods. An attacker with the capability of inserting their own data points into the training set can manipulate the inferred nearest neighbor structure. We distill this goal to the task of performing a training-set data insertion attack against $k$-Nearest Neighbor classification ($k$NN). We prove that computing an optimal training-time (a.k.a. poisoning) attack against $k$NN classification is NP-Hard, even when $k = 1$ and the attacker can insert only a single data point. We provide an anytime algorithm to perform such an attack, and a greedy algorithm for general $k$ and attacker budget. We provide theoretical bounds and empirically demonstrate the effectiveness and practicality of our methods on synthetic and real-world datasets. Empirically, we find that $k$NN is vulnerable in practice and that dimensionality reduction is an effective defense. We conclude with a discussion of open problems illuminated by our analysis.

Preference-Based Batch and Sequential Teaching

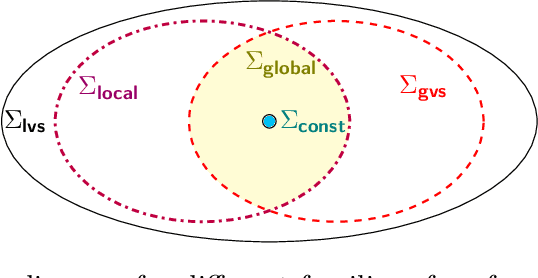
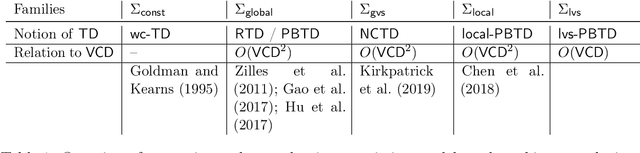
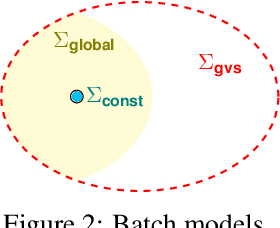
Algorithmic machine teaching studies the interaction between a teacher and a learner where the teacher selects labeled examples aiming at teaching a target hypothesis. In a quest to lower teaching complexity, several teaching models and complexity measures have been proposed for both the batch settings (e.g., worst-case, recursive, preference-based, and non-clashing models) and the sequential settings (e.g., local preference-based model). To better understand the connections between these models, we develop a novel framework that captures the teaching process via preference functions $\Sigma$. In our framework, each function $\sigma \in \Sigma$ induces a teacher-learner pair with teaching complexity as $TD(\sigma)$. We show that the above-mentioned teaching models are equivalent to specific types/families of preference functions. We analyze several properties of the teaching complexity parameter $TD(\sigma)$ associated with different families of the preference functions, e.g., comparison to the VC dimension of the hypothesis class and additivity/sub-additivity of $TD(\sigma)$ over disjoint domains. Finally, we identify preference functions inducing a novel family of sequential models with teaching complexity linear in the VC dimension: this is in contrast to the best-known complexity result for the batch models, which is quadratic in the VC dimension.

Preference-Based Batch and Sequential Teaching: Towards a Unified View of Models

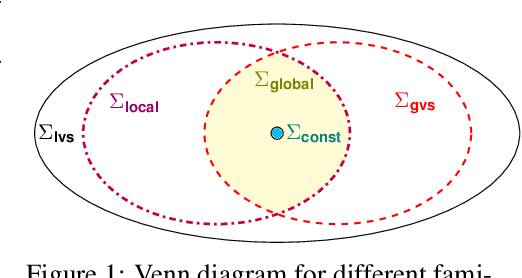
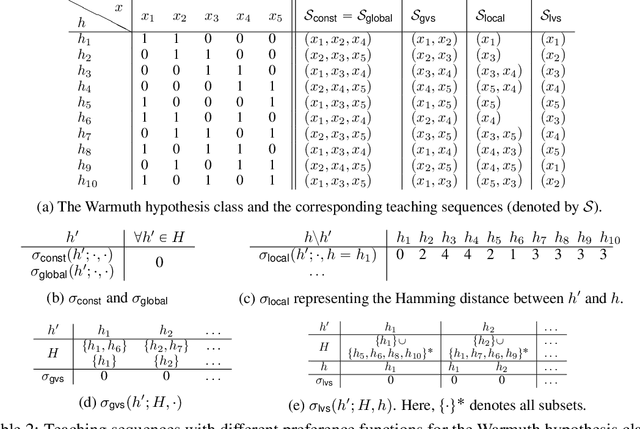
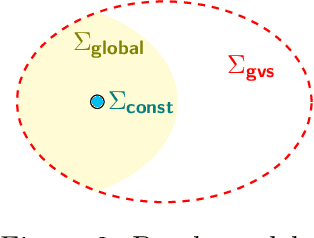
Algorithmic machine teaching studies the interaction between a teacher and a learner where the teacher selects labeled examples aiming at teaching a target hypothesis. In a quest to lower teaching complexity and to achieve more natural teacher-learner interactions, several teaching models and complexity measures have been proposed for both the batch settings (e.g., worst-case, recursive, preference-based, and non-clashing models) as well as the sequential settings (e.g., local preference-based model). To better understand the connections between these different batch and sequential models, we develop a novel framework which captures the teaching process via preference functions $\Sigma$. In our framework, each function $\sigma \in \Sigma$ induces a teacher-learner pair with teaching complexity as $\TD(\sigma)$. We show that the above-mentioned teaching models are equivalent to specific types/families of preference functions in our framework. This equivalence, in turn, allows us to study the differences between two important teaching models, namely $\sigma$ functions inducing the strongest batch (i.e., non-clashing) model and $\sigma$ functions inducing a weak sequential (i.e., local preference-based) model. Finally, we identify preference functions inducing a novel family of sequential models with teaching complexity linear in the VC dimension of the hypothesis class: this is in contrast to the best known complexity result for the batch models which is quadratic in the VC dimension.

Program Synthesis from Visual Specification

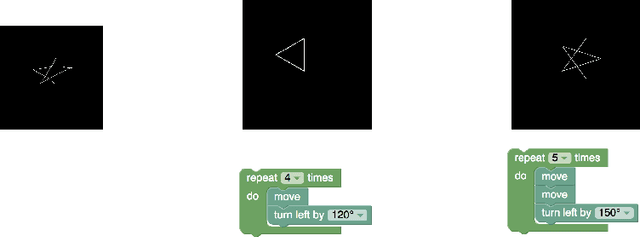
Program synthesis is the process of automatically translating a specification into computer code. Traditional synthesis settings require a formal, precise specification. Motivated by computer education applications where a student learns to code simple turtle-style drawing programs, we study a novel synthesis setting where only a noisy user-intention drawing is specified. This allows students to sketch their intended output, optionally together with their own incomplete program, to automatically produce a completed program. We formulate this synthesis problem as search in the space of programs, with the score of a state being the Hausdorff distance between the program output and the user drawing. We compare several search algorithms on a corpus consisting of real user drawings and the corresponding programs, and demonstrate that our algorithms can synthesize programs optimally satisfying the specification.