Preference-Based Batch and Sequential Teaching
Paper and Code
Oct 17, 2020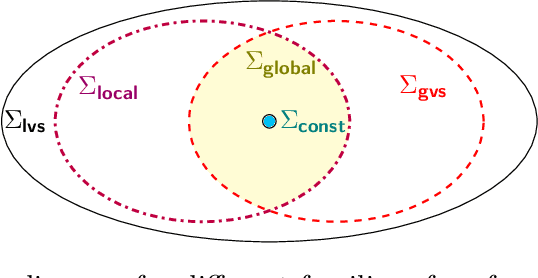
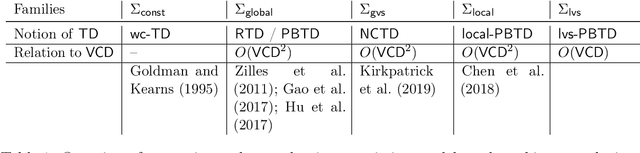
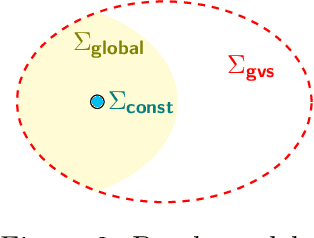

Algorithmic machine teaching studies the interaction between a teacher and a learner where the teacher selects labeled examples aiming at teaching a target hypothesis. In a quest to lower teaching complexity, several teaching models and complexity measures have been proposed for both the batch settings (e.g., worst-case, recursive, preference-based, and non-clashing models) and the sequential settings (e.g., local preference-based model). To better understand the connections between these models, we develop a novel framework that captures the teaching process via preference functions $\Sigma$. In our framework, each function $\sigma \in \Sigma$ induces a teacher-learner pair with teaching complexity as $TD(\sigma)$. We show that the above-mentioned teaching models are equivalent to specific types/families of preference functions. We analyze several properties of the teaching complexity parameter $TD(\sigma)$ associated with different families of the preference functions, e.g., comparison to the VC dimension of the hypothesis class and additivity/sub-additivity of $TD(\sigma)$ over disjoint domains. Finally, we identify preference functions inducing a novel family of sequential models with teaching complexity linear in the VC dimension: this is in contrast to the best-known complexity result for the batch models, which is quadratic in the VC dimension.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge