A Visual Active Search Framework for Geospatial Exploration

Many problems can be viewed as forms of geospatial search aided by aerial imagery, with examples ranging from detecting poaching activity to human trafficking. We model this class of problems in a visual active search (VAS) framework, which takes as input an image of a broad area, and aims to identify as many examples of a target object as possible. It does this through a limited sequence of queries, each of which verifies whether an example is present in a given region. We propose a reinforcement learning approach for VAS that leverages a collection of fully annotated search tasks as training data to learn a search policy, and combines features of the input image with a natural representation of active search state. Additionally, we propose domain adaptation techniques to improve the policy at decision time when training data is not fully reflective of the test-time distribution of VAS tasks. Through extensive experiments on several satellite imagery datasets, we show that the proposed approach significantly outperforms several strong baselines. Code and data will be made public.

Training-Time Attacks against k-Nearest Neighbors

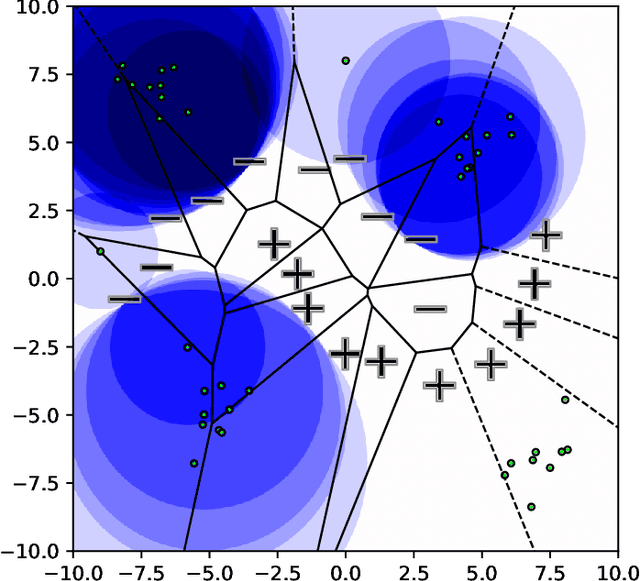
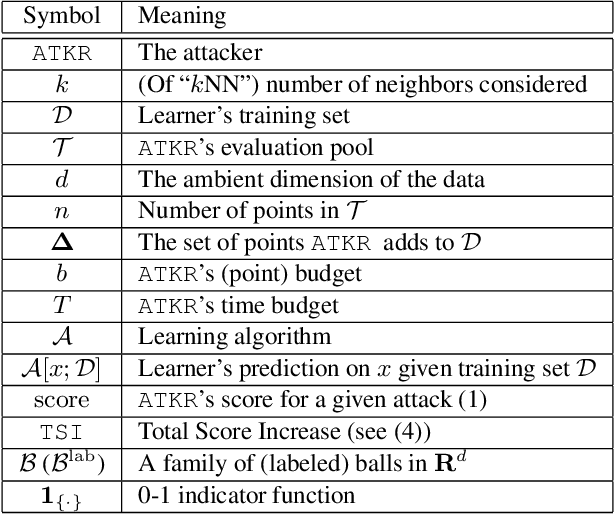
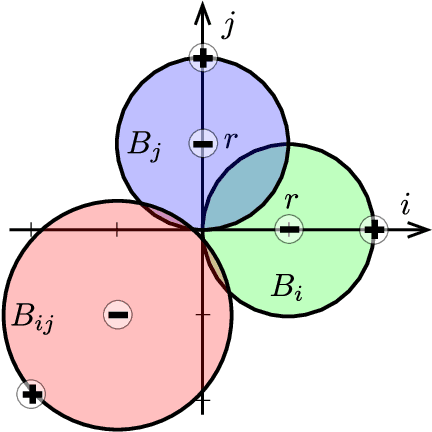
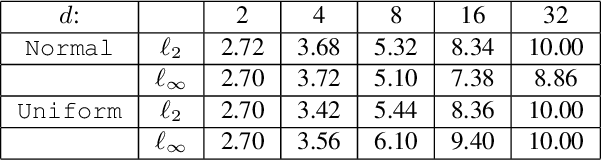
Nearest neighbor-based methods are commonly used for classification tasks and as subroutines of other data-analysis methods. An attacker with the capability of inserting their own data points into the training set can manipulate the inferred nearest neighbor structure. We distill this goal to the task of performing a training-set data insertion attack against $k$-Nearest Neighbor classification ($k$NN). We prove that computing an optimal training-time (a.k.a. poisoning) attack against $k$NN classification is NP-Hard, even when $k = 1$ and the attacker can insert only a single data point. We provide an anytime algorithm to perform such an attack, and a greedy algorithm for general $k$ and attacker budget. We provide theoretical bounds and empirically demonstrate the effectiveness and practicality of our methods on synthetic and real-world datasets. Empirically, we find that $k$NN is vulnerable in practice and that dimensionality reduction is an effective defense. We conclude with a discussion of open problems illuminated by our analysis.

Approximate Data Deletion in Generative Models

Users have the right to have their data deleted by third-party learned systems, as codified by recent legislation such as the General Data Protection Regulation (GDPR) and the California Consumer Privacy Act (CCPA). Such data deletion can be accomplished by full re-training, but this incurs a high computational cost for modern machine learning models. To avoid this cost, many approximate data deletion methods have been developed for supervised learning. Unsupervised learning, in contrast, remains largely an open problem when it comes to (approximate or exact) efficient data deletion. In this paper, we propose a density-ratio-based framework for generative models. Using this framework, we introduce a fast method for approximate data deletion and a statistical test for estimating whether or not training points have been deleted. We provide theoretical guarantees under various learner assumptions and empirically demonstrate our methods across a variety of generative methods.

Hard to Forget: Poisoning Attacks on Certified Machine Unlearning

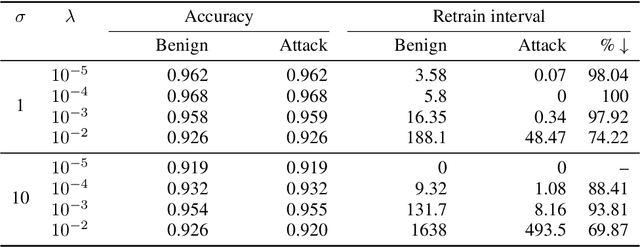
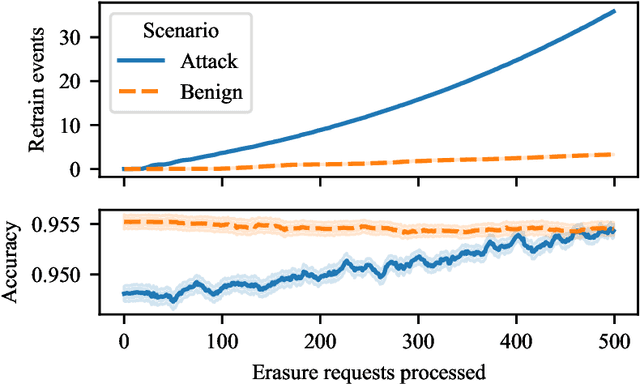
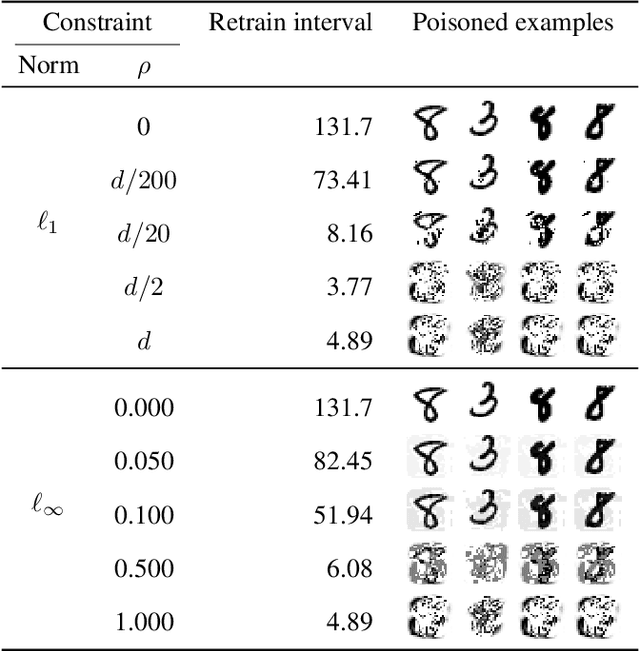
The right to erasure requires removal of a user's information from data held by organizations, with rigorous interpretations extending to downstream products such as learned models. Retraining from scratch with the particular user's data omitted fully removes its influence on the resulting model, but comes with a high computational cost. Machine "unlearning" mitigates the cost incurred by full retraining: instead, models are updated incrementally, possibly only requiring retraining when approximation errors accumulate. Rapid progress has been made towards privacy guarantees on the indistinguishability of unlearned and retrained models, but current formalisms do not place practical bounds on computation. In this paper we demonstrate how an attacker can exploit this oversight, highlighting a novel attack surface introduced by machine unlearning. We consider an attacker aiming to increase the computational cost of data removal. We derive and empirically investigate a poisoning attack on certified machine unlearning where strategically designed training data triggers complete retraining when removed.

RAWLSNET: Altering Bayesian Networks to Encode Rawlsian Fair Equality of Opportunity

We present RAWLSNET, a system for altering Bayesian Network (BN) models to satisfy the Rawlsian principle of fair equality of opportunity (FEO). RAWLSNET's BN models generate aspirational data distributions: data generated to reflect an ideally fair, FEO-satisfying society. FEO states that everyone with the same talent and willingness to use it should have the same chance of achieving advantageous social positions (e.g., employment), regardless of their background circumstances (e.g., socioeconomic status). Satisfying FEO requires alterations to social structures such as school assignments. Our paper describes RAWLSNET, a method which takes as input a BN representation of an FEO application and alters the BN's parameters so as to satisfy FEO when possible, and minimize deviation from FEO otherwise. We also offer guidance for applying RAWLSNET, including on recognizing proper applications of FEO. We demonstrate the use of our system with publicly available data sets. RAWLSNET's altered BNs offer the novel capability of generating aspirational data for FEO-relevant tasks. Aspirational data are free from the biases of real-world data, and thus are useful for recognizing and detecting sources of unfairness in machine learning algorithms besides biased data.

Optimizing Graph Structure for Targeted Diffusion

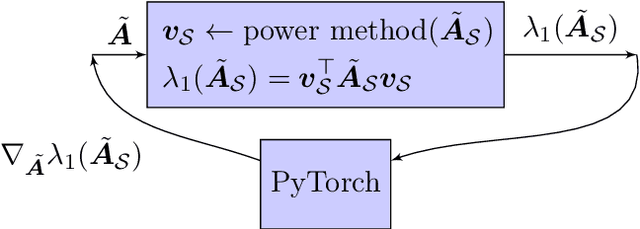
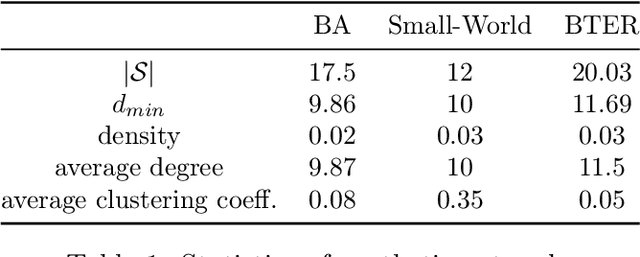
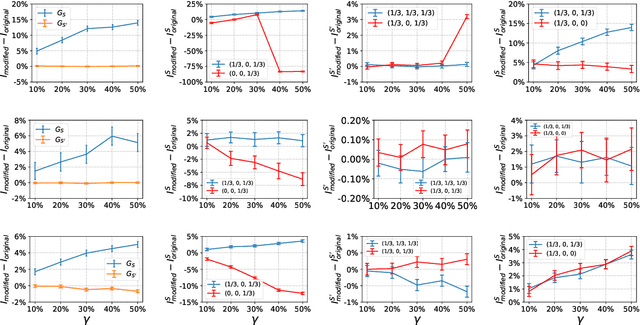
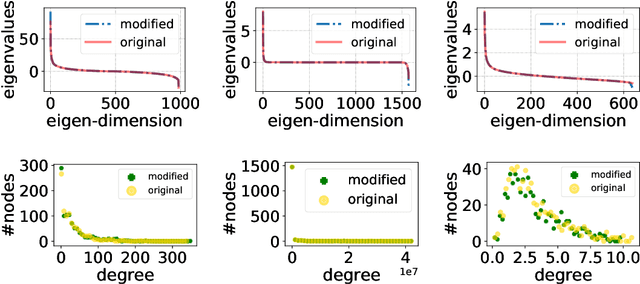
The problem of diffusion control on networks has been extensively studied, with applications ranging from marketing to cybersecurity. However, in many applications, such as targeted vulnerability assessment or clinical therapies, one aspires to affect a targeted subset of a network, while limiting the impact on the rest. We present a novel model in which the principal aim is to optimize graph structure to affect such targeted diffusion. We present an algorithmic approach for solving this problem at scale, using a gradient-based approach that leverages Rayleigh quotients and pseudospectrum theory. In addition, we present a condition for certifying a targeted subgraph as immune to targeted diffusion. Finally, we demonstrate the effectiveness of our approach through extensive experiments on real and synthetic networks.

Adversarial Regression with Multiple Learners

Despite the considerable success enjoyed by machine learning techniques in practice, numerous studies demonstrated that many approaches are vulnerable to attacks. An important class of such attacks involves adversaries changing features at test time to cause incorrect predictions. Previous investigations of this problem pit a single learner against an adversary. However, in many situations an adversary's decision is aimed at a collection of learners, rather than specifically targeted at each independently. We study the problem of adversarial linear regression with multiple learners. We approximate the resulting game by exhibiting an upper bound on learner loss functions, and show that the resulting game has a unique symmetric equilibrium. We present an algorithm for computing this equilibrium, and show through extensive experiments that equilibrium models are significantly more robust than conventional regularized linear regression.

Contamination Estimation via Convex Relaxations

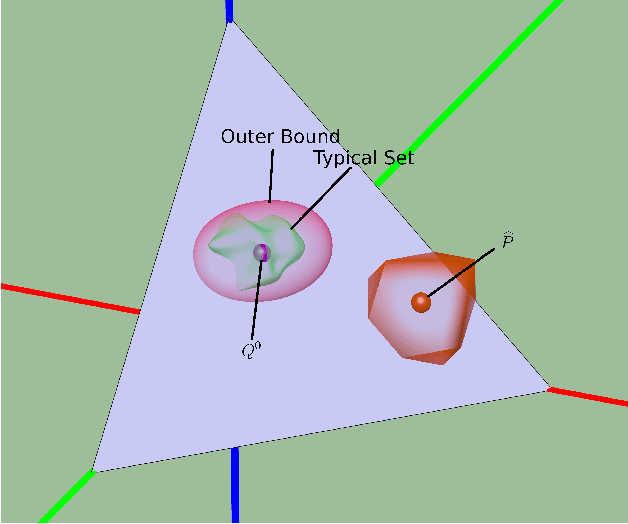
Identifying anomalies and contamination in datasets is important in a wide variety of settings. In this paper, we describe a new technique for estimating contamination in large, discrete valued datasets. Our approach considers the normal condition of the data to be specified by a model consisting of a set of distributions. Our key contribution is in our approach to contamination estimation. Specifically, we develop a technique that identifies the minimum number of data points that must be discarded (i.e., the level of contamination) from an empirical data set in order to match the model to within a specified goodness-of-fit, controlled by a p-value. Appealing to results from large deviations theory, we show a lower bound on the level of contamination is obtained by solving a series of convex programs. Theoretical results guarantee the bound converges at a rate of $O(\sqrt{\log(p)/p})$, where p is the size of the empirical data set.