Adversarial Machine Unlearning

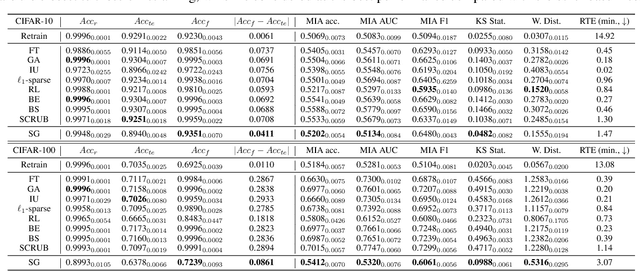
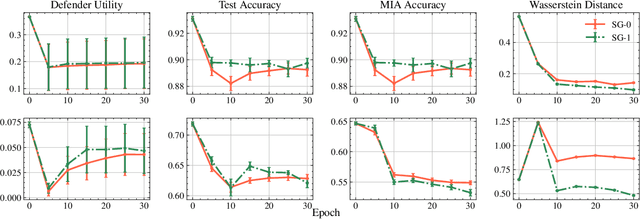
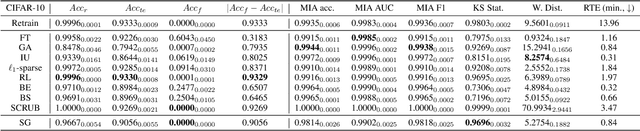
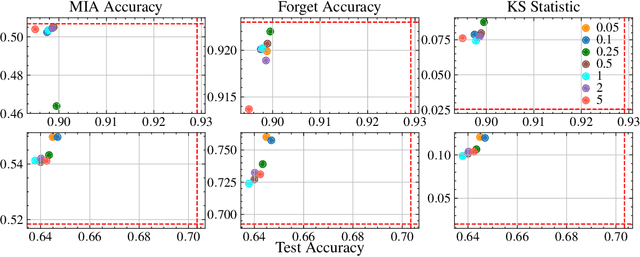
This paper focuses on the challenge of machine unlearning, aiming to remove the influence of specific training data on machine learning models. Traditionally, the development of unlearning algorithms runs parallel with that of membership inference attacks (MIA), a type of privacy threat to determine whether a data instance was used for training. However, the two strands are intimately connected: one can view machine unlearning through the lens of MIA success with respect to removed data. Recognizing this connection, we propose a game-theoretic framework that integrates MIAs into the design of unlearning algorithms. Specifically, we model the unlearning problem as a Stackelberg game in which an unlearner strives to unlearn specific training data from a model, while an auditor employs MIAs to detect the traces of the ostensibly removed data. Adopting this adversarial perspective allows the utilization of new attack advancements, facilitating the design of unlearning algorithms. Our framework stands out in two ways. First, it takes an adversarial approach and proactively incorporates the attacks into the design of unlearning algorithms. Secondly, it uses implicit differentiation to obtain the gradients that limit the attacker's success, thus benefiting the process of unlearning. We present empirical results to demonstrate the effectiveness of the proposed approach for machine unlearning.

Altruism Design in Networked Public Goods Games

Many collective decision-making settings feature a strategic tension between agents acting out of individual self-interest and promoting a common good. These include wearing face masks during a pandemic, voting, and vaccination. Networked public goods games capture this tension, with networks encoding strategic interdependence among agents. Conventional models of public goods games posit solely individual self-interest as a motivation, even though altruistic motivations have long been known to play a significant role in agents' decisions. We introduce a novel extension of public goods games to account for altruistic motivations by adding a term in the utility function that incorporates the perceived benefits an agent obtains from the welfare of others, mediated by an altruism graph. Most importantly, we view altruism not as immutable, but rather as a lever for promoting the common good. Our central algorithmic question then revolves around the computational complexity of modifying the altruism network to achieve desired public goods game investment profiles. We first show that the problem can be solved using linear programming when a principal can fractionally modify the altruism network. While the problem becomes in general intractable if the principal's actions are all-or-nothing, we exhibit several tractable special cases.

Optimizing Graph Structure for Targeted Diffusion

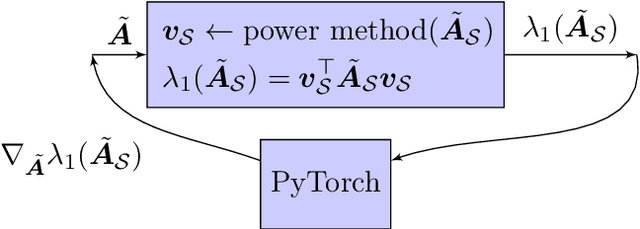
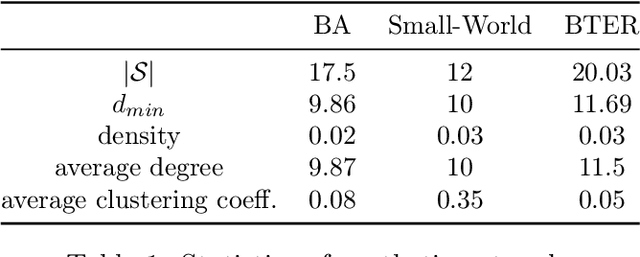
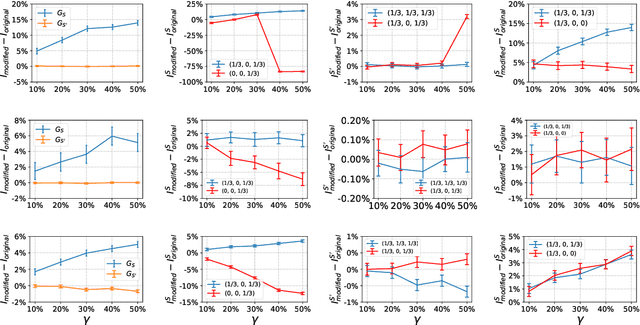
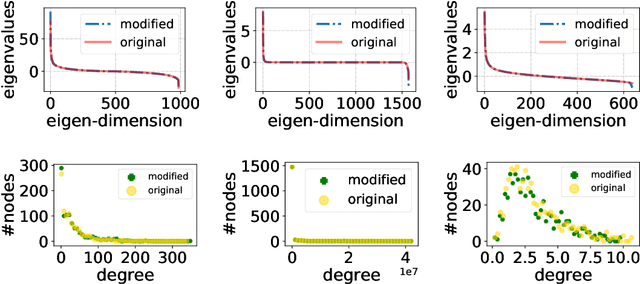
The problem of diffusion control on networks has been extensively studied, with applications ranging from marketing to cybersecurity. However, in many applications, such as targeted vulnerability assessment or clinical therapies, one aspires to affect a targeted subset of a network, while limiting the impact on the rest. We present a novel model in which the principal aim is to optimize graph structure to affect such targeted diffusion. We present an algorithmic approach for solving this problem at scale, using a gradient-based approach that leverages Rayleigh quotients and pseudospectrum theory. In addition, we present a condition for certifying a targeted subgraph as immune to targeted diffusion. Finally, we demonstrate the effectiveness of our approach through extensive experiments on real and synthetic networks.

Inducing Equilibria in Networked Public Goods Games through Network Structure Modification

Networked public goods games model scenarios in which self-interested agents decide whether or how much to invest in an action that benefits not only themselves, but also their network neighbors. Examples include vaccination, security investment, and crime reporting. While every agent's utility is increasing in their neighbors' joint investment, the specific form can vary widely depending on the scenario. A principal, such as a policymaker, may wish to induce large investment from the agents. Besides direct incentives, an important lever here is the network structure itself: by adding and removing edges, for example, through community meetings, the principal can change the nature of the utility functions, resulting in different, and perhaps socially preferable, equilibrium outcomes. We initiate an algorithmic study of targeted network modifications with the goal of inducing equilibria of a particular form. We study this question for a variety of equilibrium forms (induce all agents to invest, at least a given set $S$, exactly a given set $S$, at least $k$ agents), and for a variety of utility functions. While we show that the problem is NP-complete for a number of these scenarios, we exhibit a broad array of scenarios in which the problem can be solved in polynomial time by non-trivial reductions to (minimum-cost) matching problems.

Computing Equilibria in Binary Networked Public Goods Games

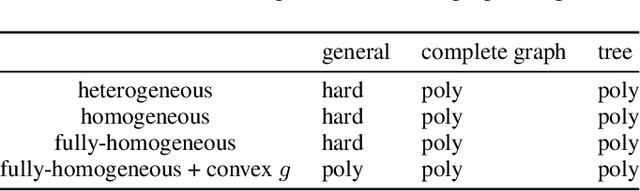
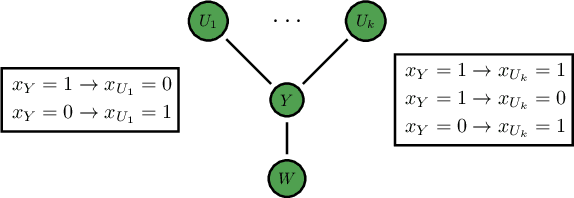
Public goods games study the incentives of individuals to contribute to a public good and their behaviors in equilibria. In this paper, we examine a specific type of public goods game where players are networked and each has binary actions, and focus on the algorithmic aspects of such games. First, we show that checking the existence of a pure-strategy Nash equilibrium is NP-Complete. We then identify tractable instances based on restrictions of either utility functions or of the underlying graphical structure. In certain cases, we also show that we can efficiently compute a socially optimal Nash equilibrium. Finally, we propose a heuristic approach for computing approximate equilibria in general binary networked public goods games, and experimentally demonstrate its effectiveness.

Distributionally Robust Removal of Malicious Nodes from Networks

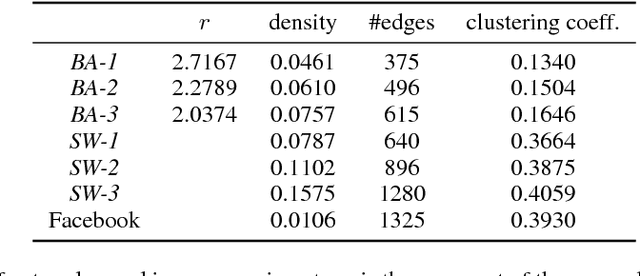
An important problem in networked systems is detection and removal of suspected malicious nodes. A crucial consideration in such settings is the uncertainty endemic in detection, coupled with considerations of network connectivity, which impose indirect costs from mistakely removing benign nodes as well as failing to remove malicious nodes. A recent approach proposed to address this problem directly tackles these considerations, but has a significant limitation: it assumes that the decision maker has accurate knowledge of the joint maliciousness probability of the nodes on the network. This is clearly not the case in practice, where such a distribution is at best an estimate from limited evidence. To address this problem, we propose a distributionally robust framework for optimal node removal. While the problem is NP-Hard, we propose a principled algorithmic technique for solving it approximately based on duality combined with Semidefinite Programming relaxation. A combination of both theoretical and empirical analysis, the latter using both synthetic and real data, provide strong evidence that our algorithmic approach is highly effective and, in particular, is significantly more robust than the state of the art.

Removing Malicious Nodes from Networks

A fundamental challenge in networked systems is detection and removal of suspected malicious nodes. In reality, detection is always imperfect, and the decision about which potentially malicious nodes to remove must trade off false positives (erroneously removing benign nodes) and false negatives (mistakenly failing to remove malicious nodes). However, in network settings this conventional tradeoff must now account for node connectivity. In particular, malicious nodes may exert malicious influence, so that mistakenly leaving some of these in the network may cause damage to spread. On the other hand, removing benign nodes causes direct harm to these, and indirect harm to their benign neighbors who would wish to communicate with them. We formalize the problem of removing potentially malicious nodes from a network under uncertainty through an objective that takes connectivity into account. We show that optimally solving the resulting problem is NP-Hard. We then propose a tractable solution approach based on a convex relaxation of the objective. Finally, we experimentally demonstrate that our approach significantly outperforms both a simple baseline that ignores network structure, as well as a state-of-the-art approach for a related problem, on both synthetic and real-world datasets.

Adversarial Regression with Multiple Learners

Despite the considerable success enjoyed by machine learning techniques in practice, numerous studies demonstrated that many approaches are vulnerable to attacks. An important class of such attacks involves adversaries changing features at test time to cause incorrect predictions. Previous investigations of this problem pit a single learner against an adversary. However, in many situations an adversary's decision is aimed at a collection of learners, rather than specifically targeted at each independently. We study the problem of adversarial linear regression with multiple learners. We approximate the resulting game by exhibiting an upper bound on learner loss functions, and show that the resulting game has a unique symmetric equilibrium. We present an algorithm for computing this equilibrium, and show through extensive experiments that equilibrium models are significantly more robust than conventional regularized linear regression.