Distributionally Robust Removal of Malicious Nodes from Networks
Paper and Code
Jan 31, 2019
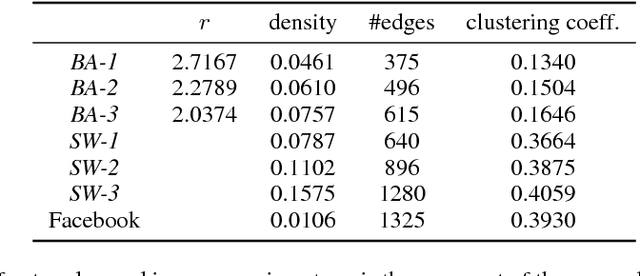


An important problem in networked systems is detection and removal of suspected malicious nodes. A crucial consideration in such settings is the uncertainty endemic in detection, coupled with considerations of network connectivity, which impose indirect costs from mistakely removing benign nodes as well as failing to remove malicious nodes. A recent approach proposed to address this problem directly tackles these considerations, but has a significant limitation: it assumes that the decision maker has accurate knowledge of the joint maliciousness probability of the nodes on the network. This is clearly not the case in practice, where such a distribution is at best an estimate from limited evidence. To address this problem, we propose a distributionally robust framework for optimal node removal. While the problem is NP-Hard, we propose a principled algorithmic technique for solving it approximately based on duality combined with Semidefinite Programming relaxation. A combination of both theoretical and empirical analysis, the latter using both synthetic and real data, provide strong evidence that our algorithmic approach is highly effective and, in particular, is significantly more robust than the state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge