Optimizing Graph Structure for Targeted Diffusion

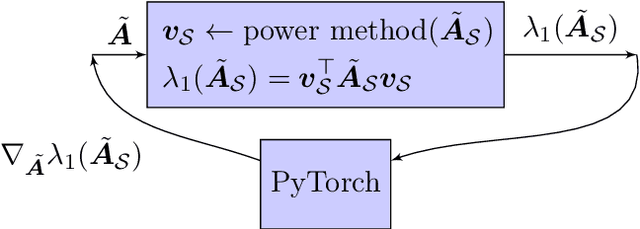
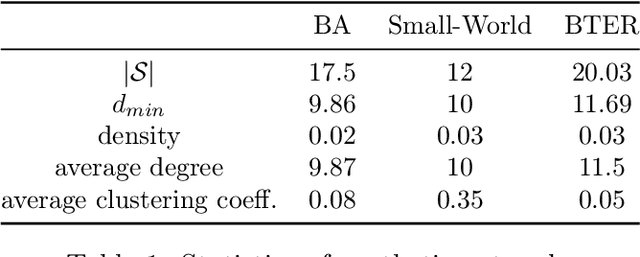
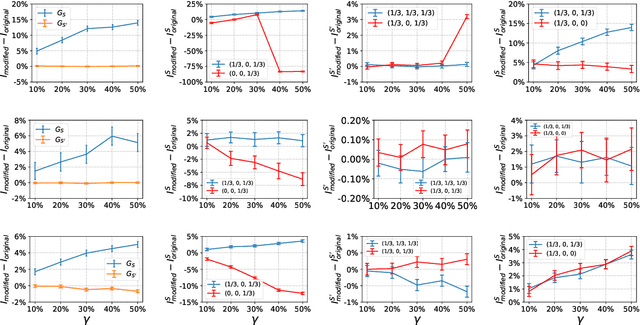
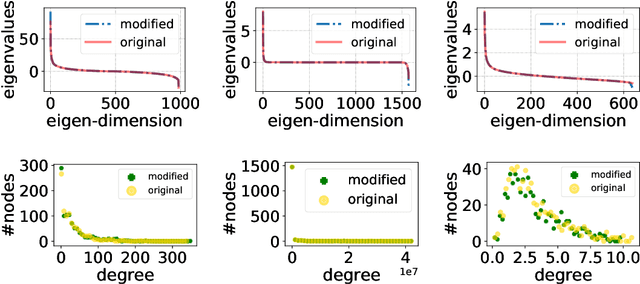
The problem of diffusion control on networks has been extensively studied, with applications ranging from marketing to cybersecurity. However, in many applications, such as targeted vulnerability assessment or clinical therapies, one aspires to affect a targeted subset of a network, while limiting the impact on the rest. We present a novel model in which the principal aim is to optimize graph structure to affect such targeted diffusion. We present an algorithmic approach for solving this problem at scale, using a gradient-based approach that leverages Rayleigh quotients and pseudospectrum theory. In addition, we present a condition for certifying a targeted subgraph as immune to targeted diffusion. Finally, we demonstrate the effectiveness of our approach through extensive experiments on real and synthetic networks.