Optimal Confidence Regions for the Multinomial Parameter

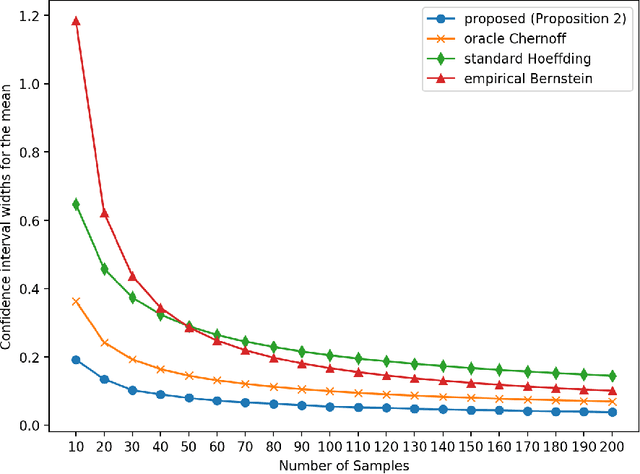
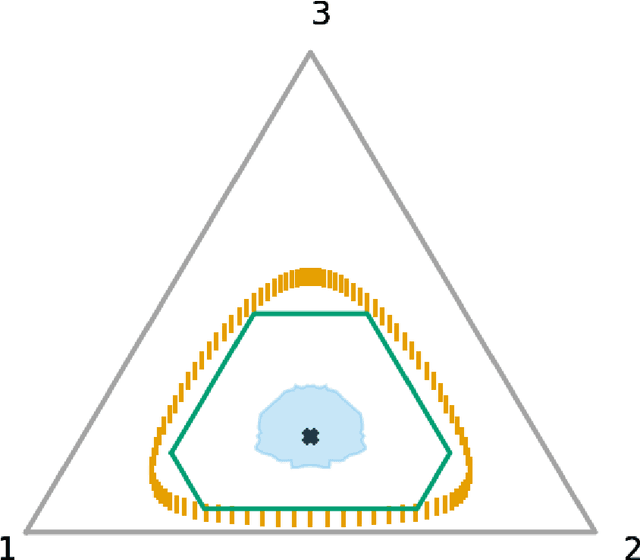
Construction of tight confidence regions and intervals is central to statistical inference and decision-making. Consider an empirical distribution $\widehat{\boldsymbol{p}}$ generated from $n$ iid realizations of a random variable that takes one of $k$ possible values according to an unknown distribution $\boldsymbol{p}$. This is analogous with a single draw from a multinomial distribution. A confidence region is a subset of the probability simplex that depends on $\widehat{\boldsymbol{p}}$ and contains the unknown $\boldsymbol{p}$ with a specified confidence. This paper shows how one can construct minimum average volume confidence regions, answering a long standing question. We also show the optimality of the regions directly translates to optimal confidence intervals of functionals, such as the mean, variance and median.

Contamination Estimation via Convex Relaxations

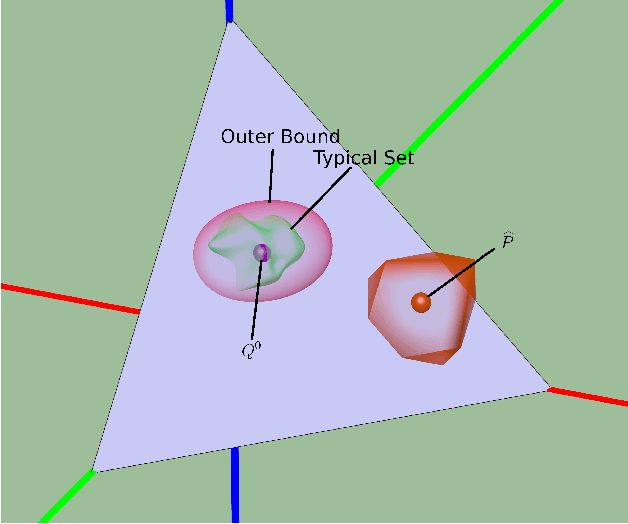
Identifying anomalies and contamination in datasets is important in a wide variety of settings. In this paper, we describe a new technique for estimating contamination in large, discrete valued datasets. Our approach considers the normal condition of the data to be specified by a model consisting of a set of distributions. Our key contribution is in our approach to contamination estimation. Specifically, we develop a technique that identifies the minimum number of data points that must be discarded (i.e., the level of contamination) from an empirical data set in order to match the model to within a specified goodness-of-fit, controlled by a p-value. Appealing to results from large deviations theory, we show a lower bound on the level of contamination is obtained by solving a series of convex programs. Theoretical results guarantee the bound converges at a rate of $O(\sqrt{\log(p)/p})$, where p is the size of the empirical data set.

Near-Optimal Adaptive Compressed Sensing

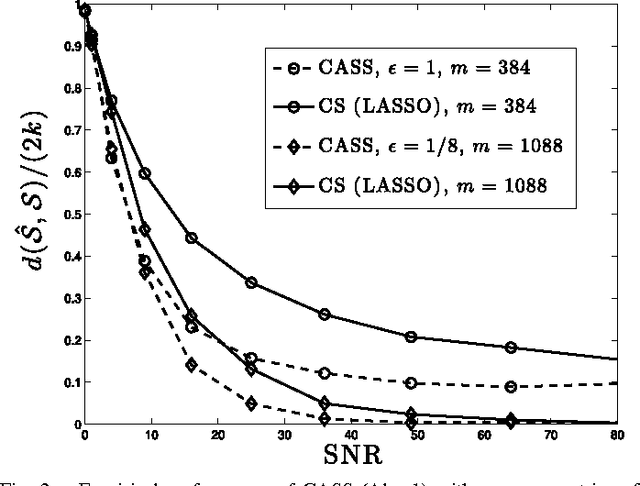
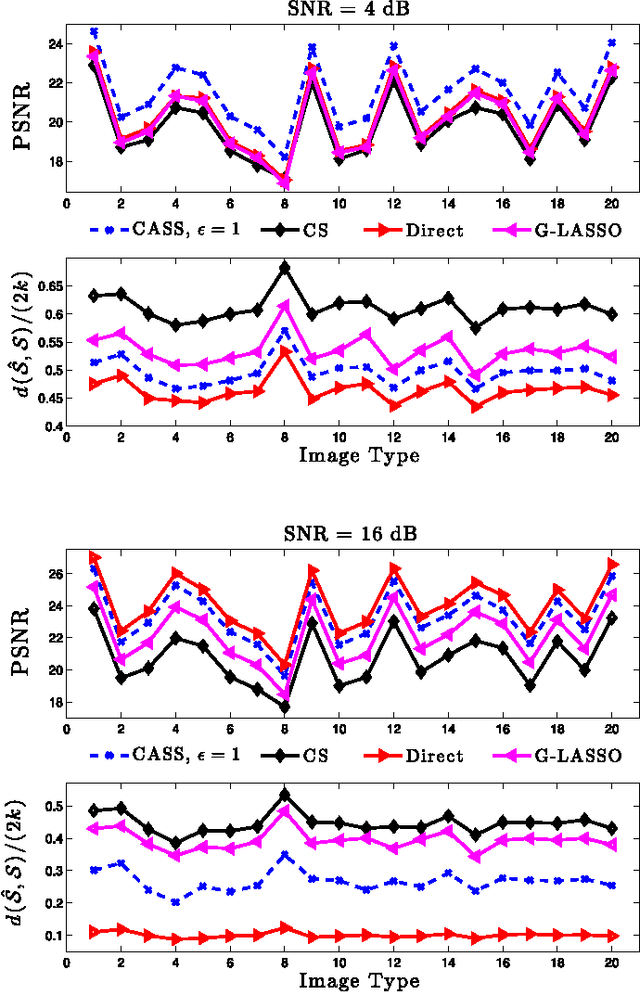
This paper proposes a simple adaptive sensing and group testing algorithm for sparse signal recovery. The algorithm, termed Compressive Adaptive Sense and Search (CASS), is shown to be near-optimal in that it succeeds at the lowest possible signal-to-noise-ratio (SNR) levels, improving on previous work in adaptive compressed sensing. Like traditional compressed sensing based on random non-adaptive design matrices, the CASS algorithm requires only k log n measurements to recover a k-sparse signal of dimension n. However, CASS succeeds at SNR levels that are a factor log n less than required by standard compressed sensing. From the point of view of constructing and implementing the sensing operation as well as computing the reconstruction, the proposed algorithm is substantially less computationally intensive than standard compressed sensing. CASS is also demonstrated to perform considerably better in practice through simulation. To the best of our knowledge, this is the first demonstration of an adaptive compressed sensing algorithm with near-optimal theoretical guarantees and excellent practical performance. This paper also shows that methods like compressed sensing, group testing, and pooling have an advantage beyond simply reducing the number of measurements or tests -- adaptive versions of such methods can also improve detection and estimation performance when compared to non-adaptive direct (uncompressed) sensing.

The Sample Complexity of Search over Multiple Populations

This paper studies the sample complexity of searching over multiple populations. We consider a large number of populations, each corresponding to either distribution P0 or P1. The goal of the search problem studied here is to find one population corresponding to distribution P1 with as few samples as possible. The main contribution is to quantify the number of samples needed to correctly find one such population. We consider two general approaches: non-adaptive sampling methods, which sample each population a predetermined number of times until a population following P1 is found, and adaptive sampling methods, which employ sequential sampling schemes for each population. We first derive a lower bound on the number of samples required by any sampling scheme. We then consider an adaptive procedure consisting of a series of sequential probability ratio tests, and show it comes within a constant factor of the lower bound. We give explicit expressions for this constant when samples of the populations follow Gaussian and Bernoulli distributions. An alternative adaptive scheme is discussed which does not require full knowledge of P1, and comes within a constant factor of the optimal scheme. For comparison, a lower bound on the sampling requirements of any non-adaptive scheme is presented.