Optimal Confidence Regions for the Multinomial Parameter

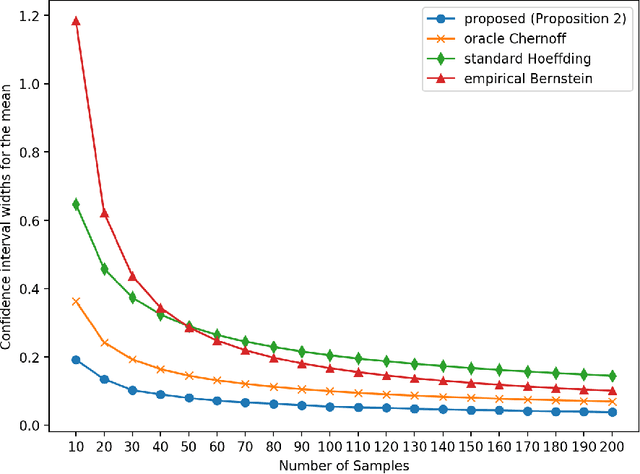
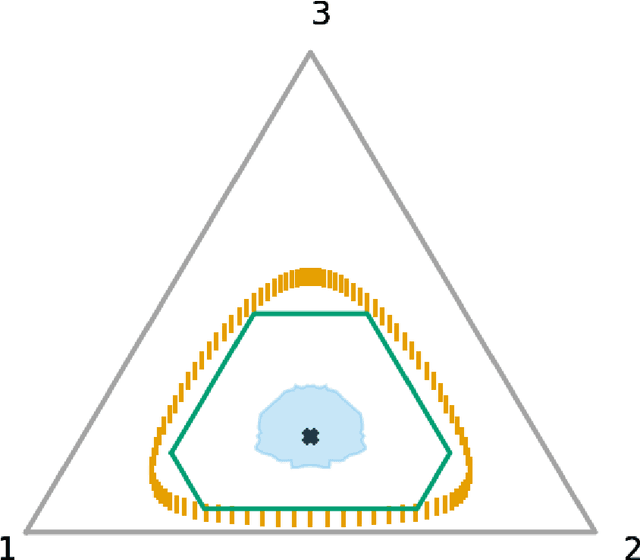
Construction of tight confidence regions and intervals is central to statistical inference and decision-making. Consider an empirical distribution $\widehat{\boldsymbol{p}}$ generated from $n$ iid realizations of a random variable that takes one of $k$ possible values according to an unknown distribution $\boldsymbol{p}$. This is analogous with a single draw from a multinomial distribution. A confidence region is a subset of the probability simplex that depends on $\widehat{\boldsymbol{p}}$ and contains the unknown $\boldsymbol{p}$ with a specified confidence. This paper shows how one can construct minimum average volume confidence regions, answering a long standing question. We also show the optimality of the regions directly translates to optimal confidence intervals of functionals, such as the mean, variance and median.