Paul Barford
Contamination Estimation via Convex Relaxations
Jun 13, 2015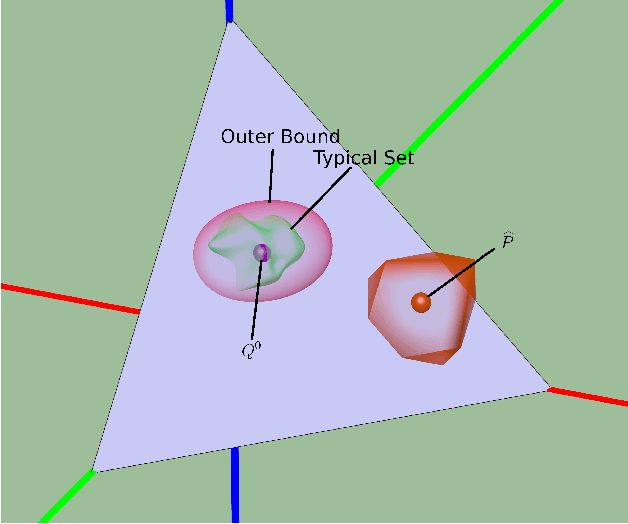

Abstract:Identifying anomalies and contamination in datasets is important in a wide variety of settings. In this paper, we describe a new technique for estimating contamination in large, discrete valued datasets. Our approach considers the normal condition of the data to be specified by a model consisting of a set of distributions. Our key contribution is in our approach to contamination estimation. Specifically, we develop a technique that identifies the minimum number of data points that must be discarded (i.e., the level of contamination) from an empirical data set in order to match the model to within a specified goodness-of-fit, controlled by a p-value. Appealing to results from large deviations theory, we show a lower bound on the level of contamination is obtained by solving a series of convex programs. Theoretical results guarantee the bound converges at a rate of $O(\sqrt{\log(p)/p})$, where p is the size of the empirical data set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge